5年级上册数学



























































来源:网络
 有用
有用
第一单元 小数乘法
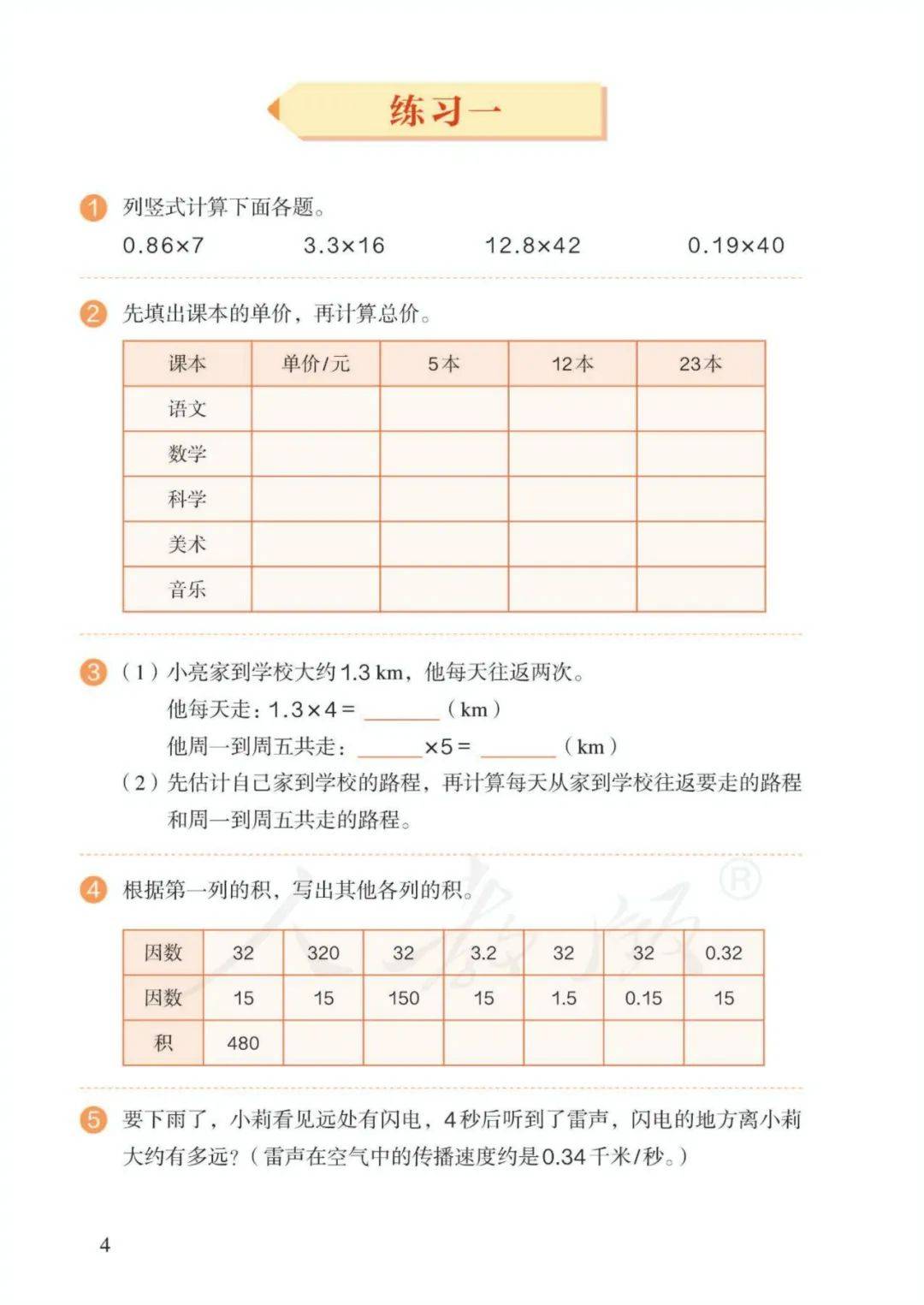
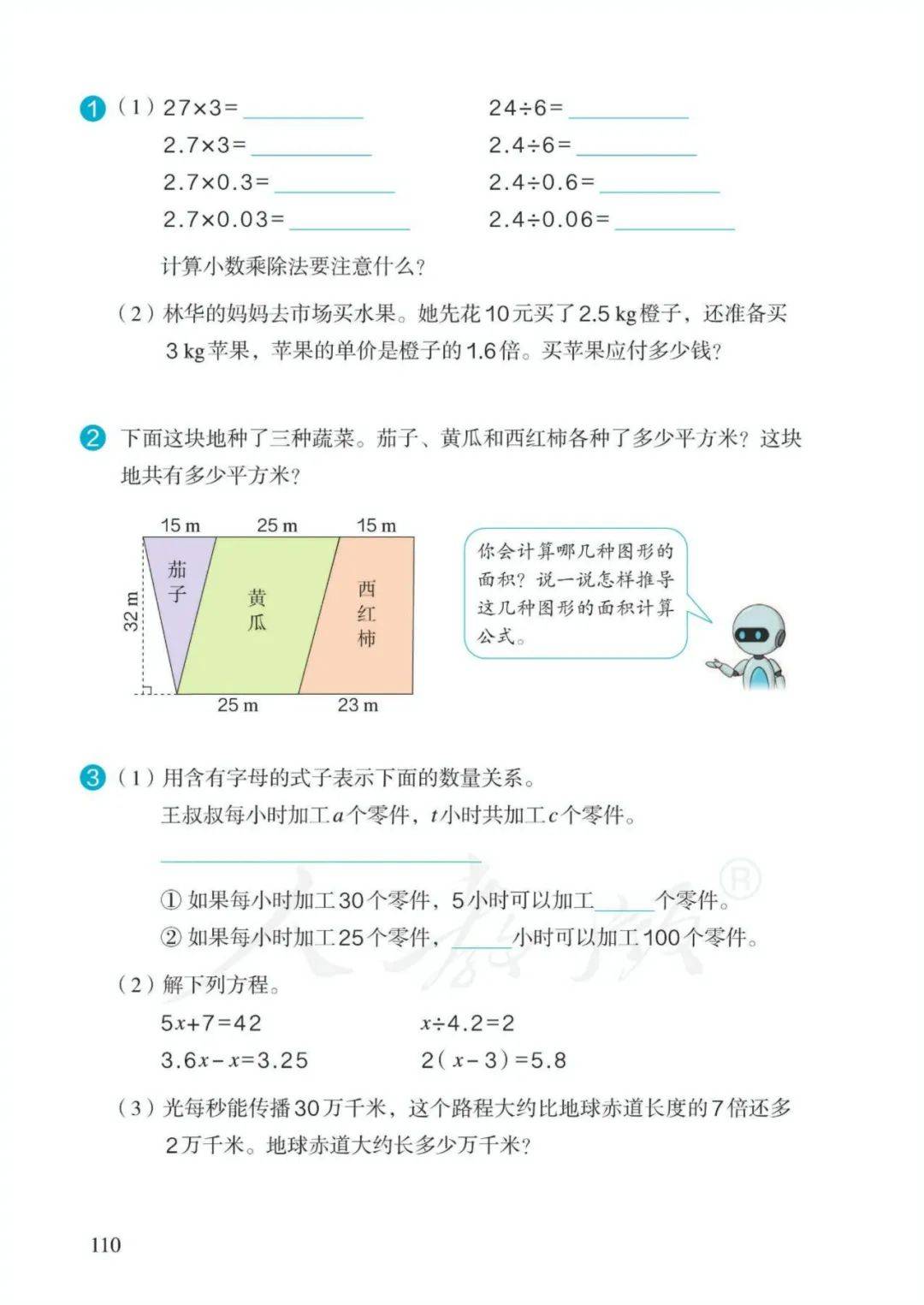
1、小数乘整数:意义——求几个相同加数的和的简便运算。如:1.5×3表示求3个1.5的和的简便运算(或1.5的3倍是多少)。
2、 计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。

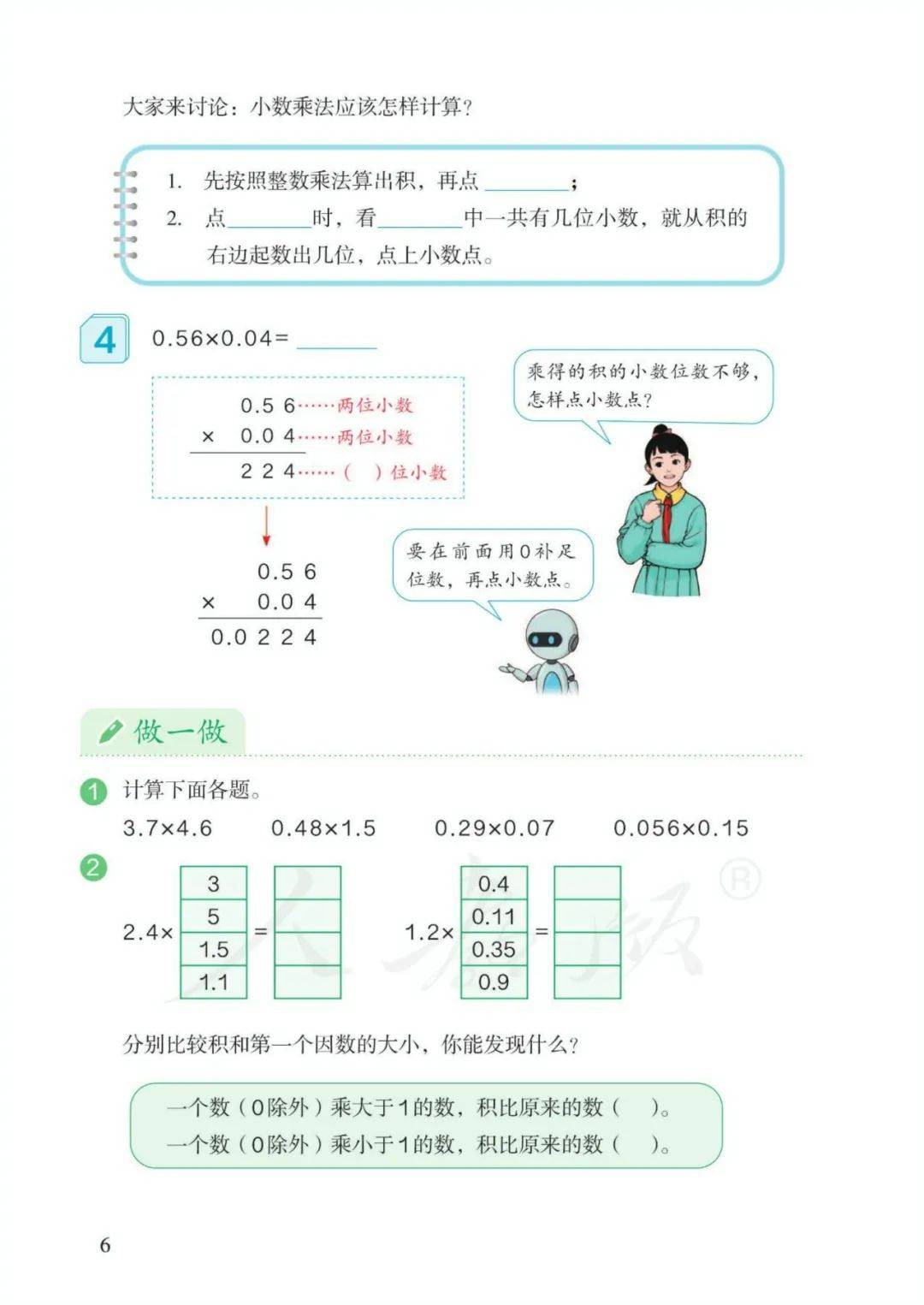
3、小数乘小数:
意义——就是求这个数的几分之几是多少。如:1.5×0.8就是求1.5的十分之八是多少(或求1.5的0.8倍是多少)。
计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
注意:按整数算出积后,小数末尾的0要去掉,也就是把小数化简;位数不够时,要用0占位。
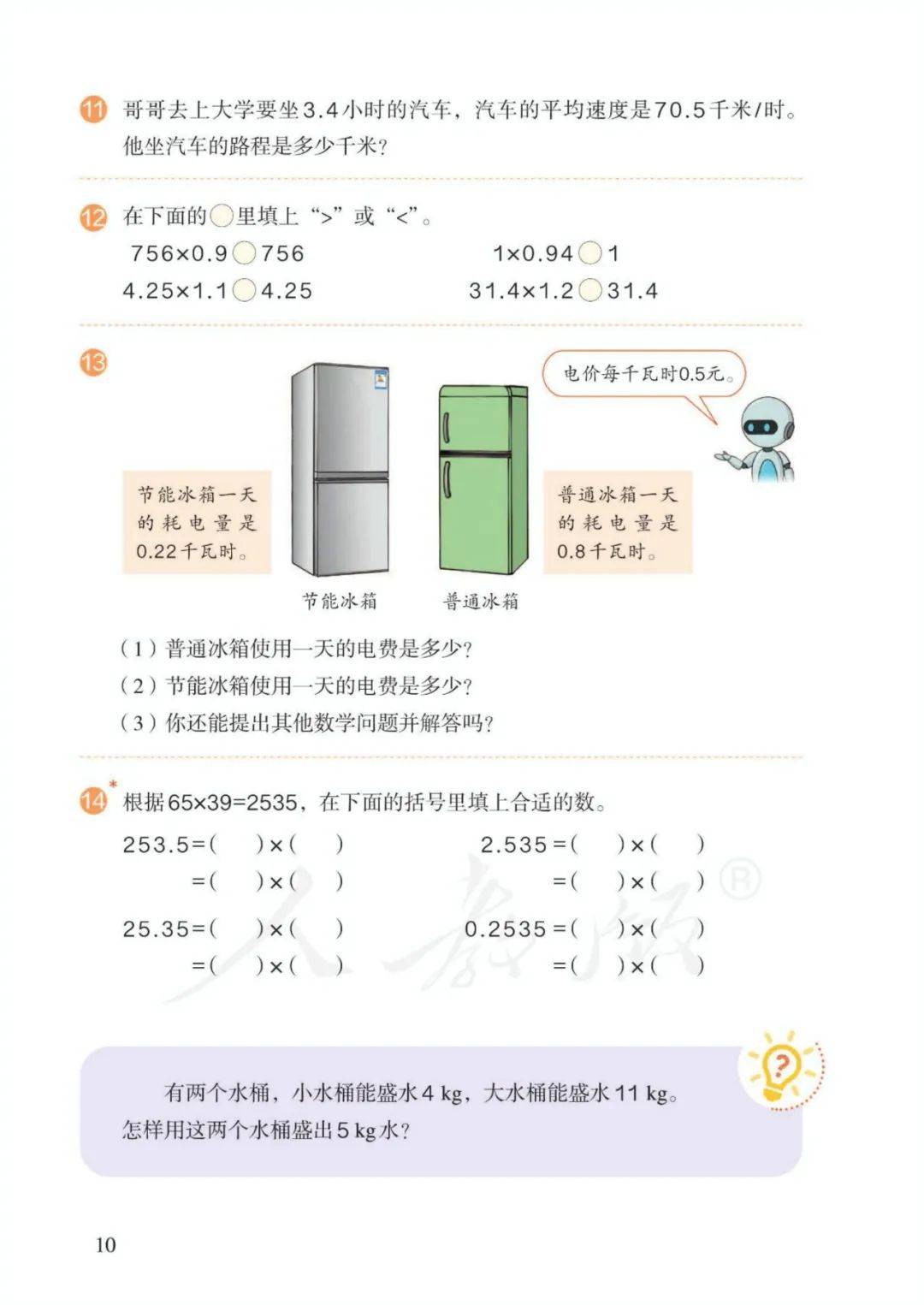
4、规律:一个数(0除外)乘大于1的数,积比原来的数大;一个数(0除外)乘小于1的数,积比原来的数小。
5、求近似数的方法一般有三种:⑴四舍五入法; ⑵进一法;⑶去尾法
6、计算钱数,保留两位小数,表示计算到分;保留一位小数,表示计算到角。
7、小数四则运算顺序和运算定律跟整数是一样的。

8、运算定律和性质:
加法:加法交换律,a+b=b+a;加法结合律:(a+b)+c=a+(b+c)
减法:a-b-c=a-(b+c) a-(b+c)=a-b-c
乘法:乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c【(a-b)×c=a×c-b×c】
除法:a÷b÷c=a÷(b×c) a÷(b×c) =a÷b÷c
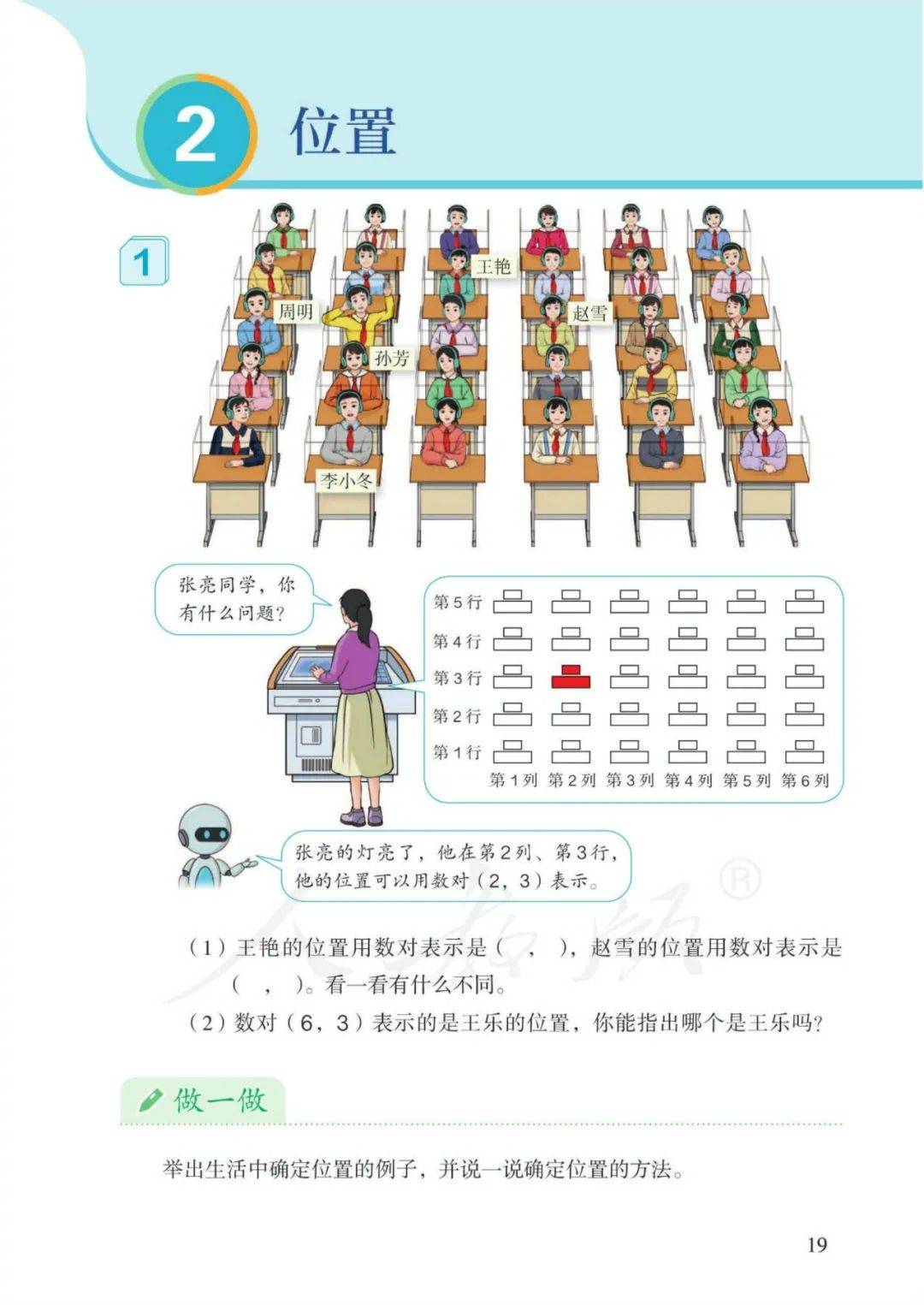
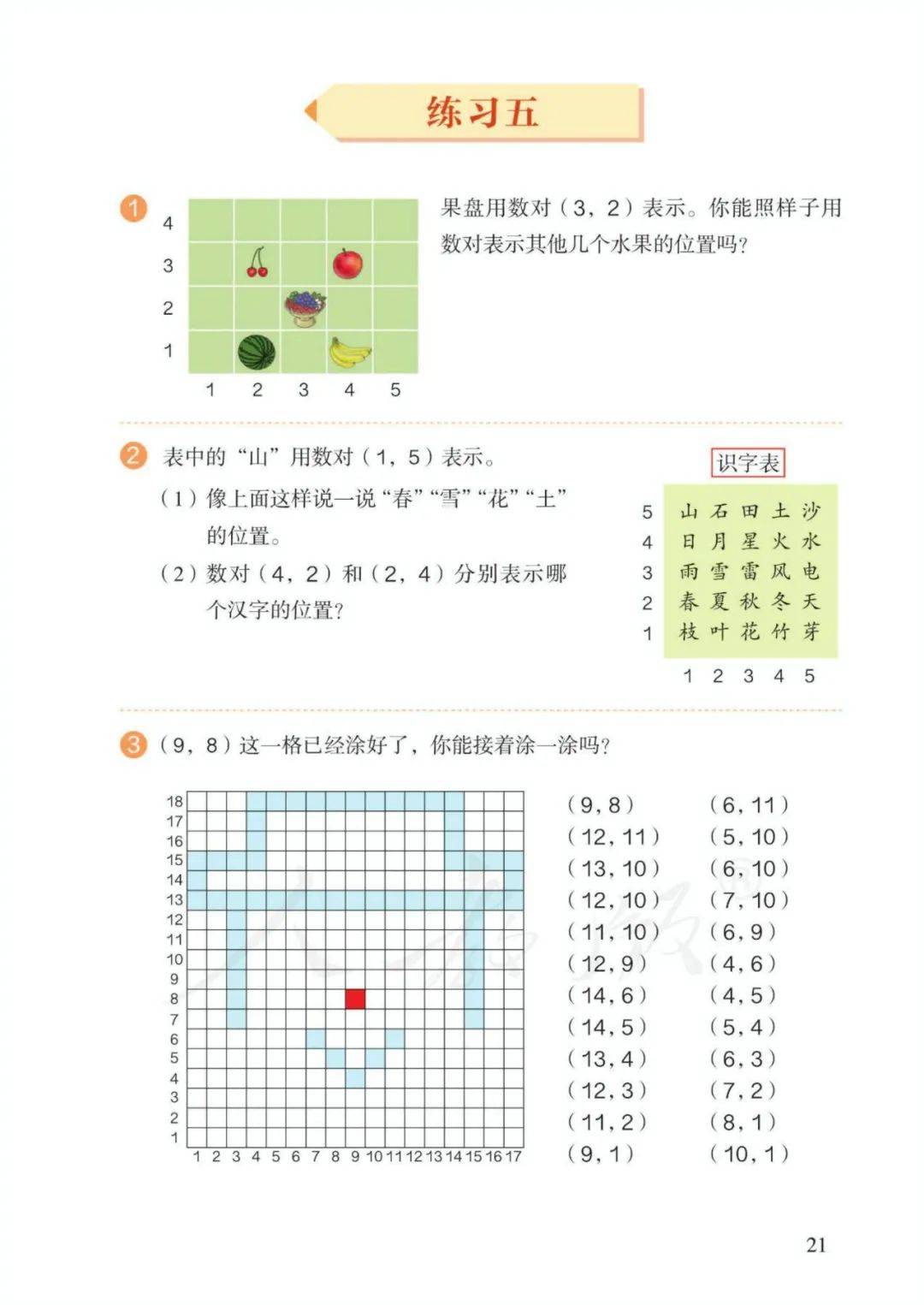
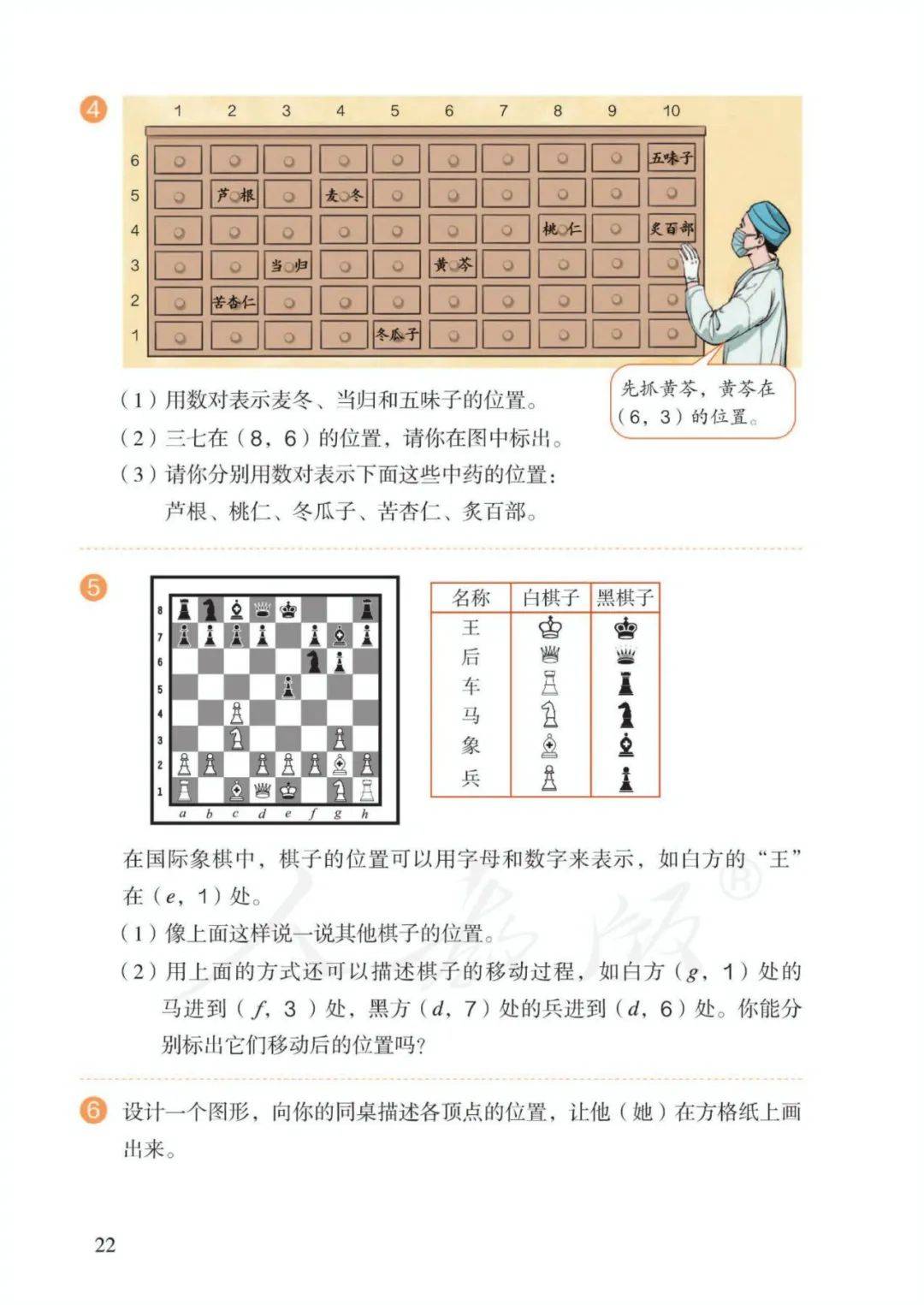
第二单元 位 置
1、数对:由两个数组成,中间用逗号隔开,用括号括起来。括号里面的数由左至右分别为列数和行数,即“先列后行”。
2、作用:一组数对确定唯一 一个点的位置。
例:在方格图(平面直角坐标系)中用数对(3,5)表示(第三列,第五行)。
注:(1)如:数对(3,2)表示第三列,第二行。
(2)数对(X,5)的行号不变,表示一条横线,(5,Y)的列号不变,表示一条竖线。(有一个数不确定,不能确定一个点)
3、 图形左右平移行数不变;图形上下平移列数不变。

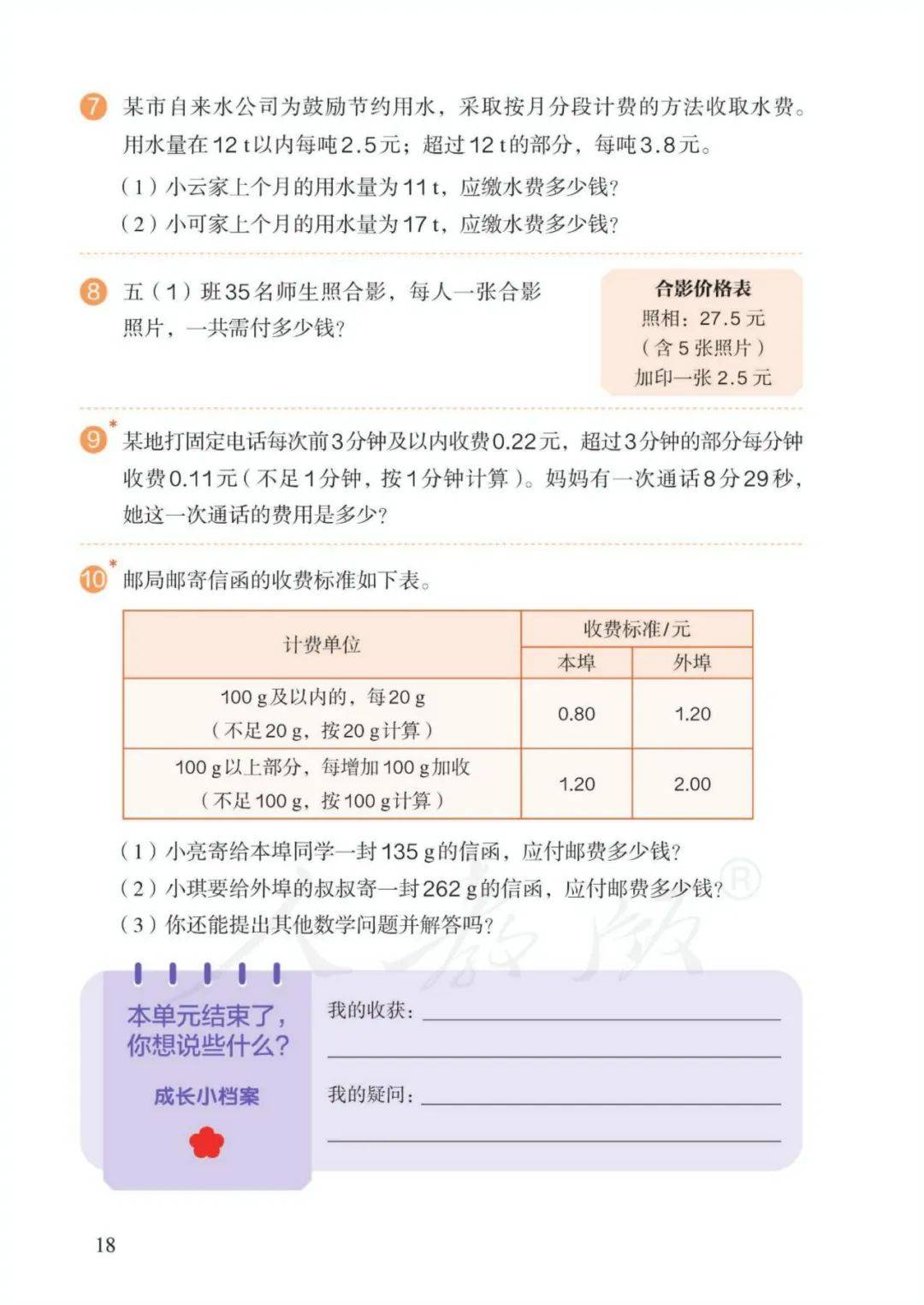
第三单元 小数除法
1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算。
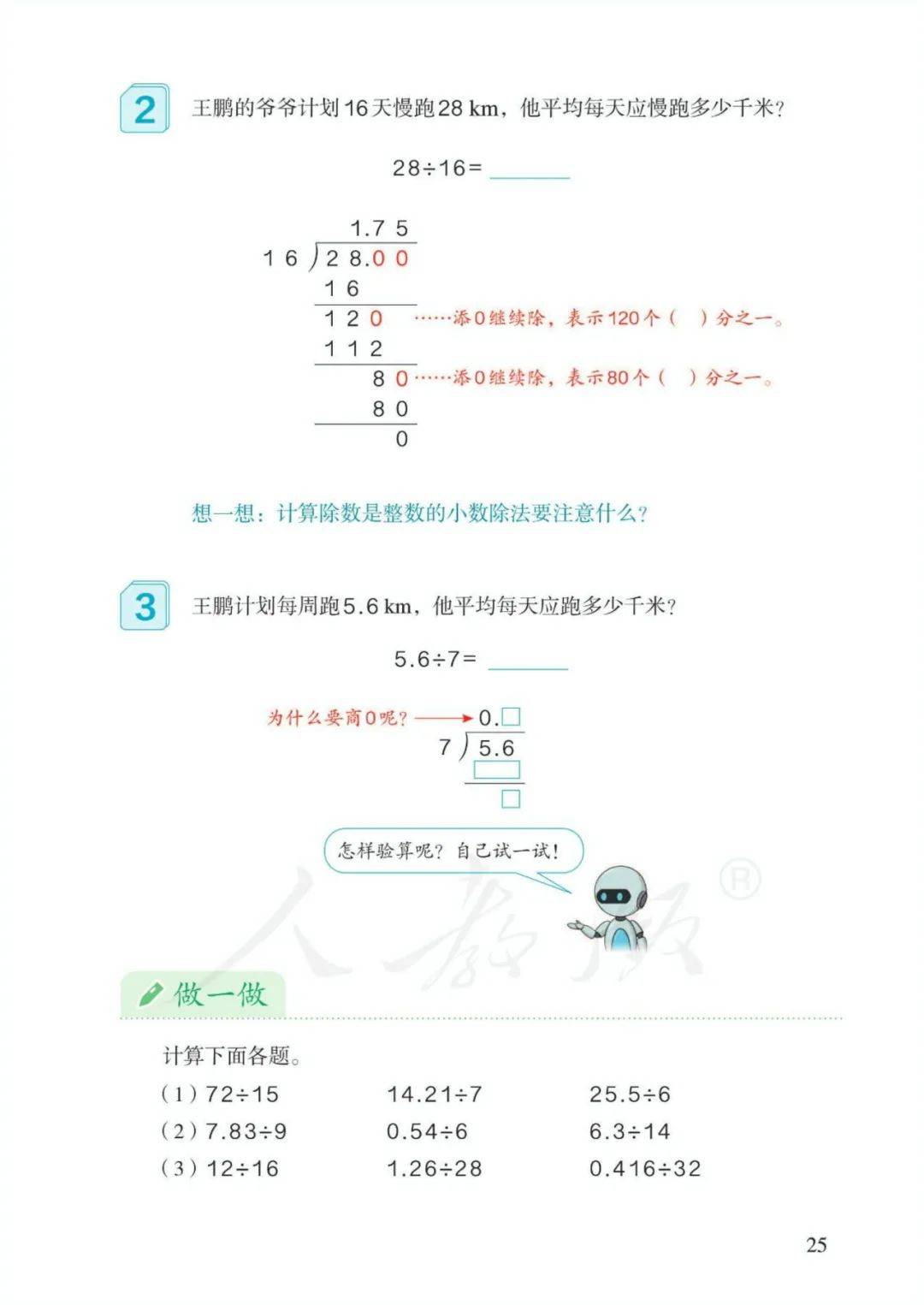
2、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除。商的小数点要和被除数的小数点对齐。整数部分不够除,商0,点上小数点。如果有余数,要添0再除。
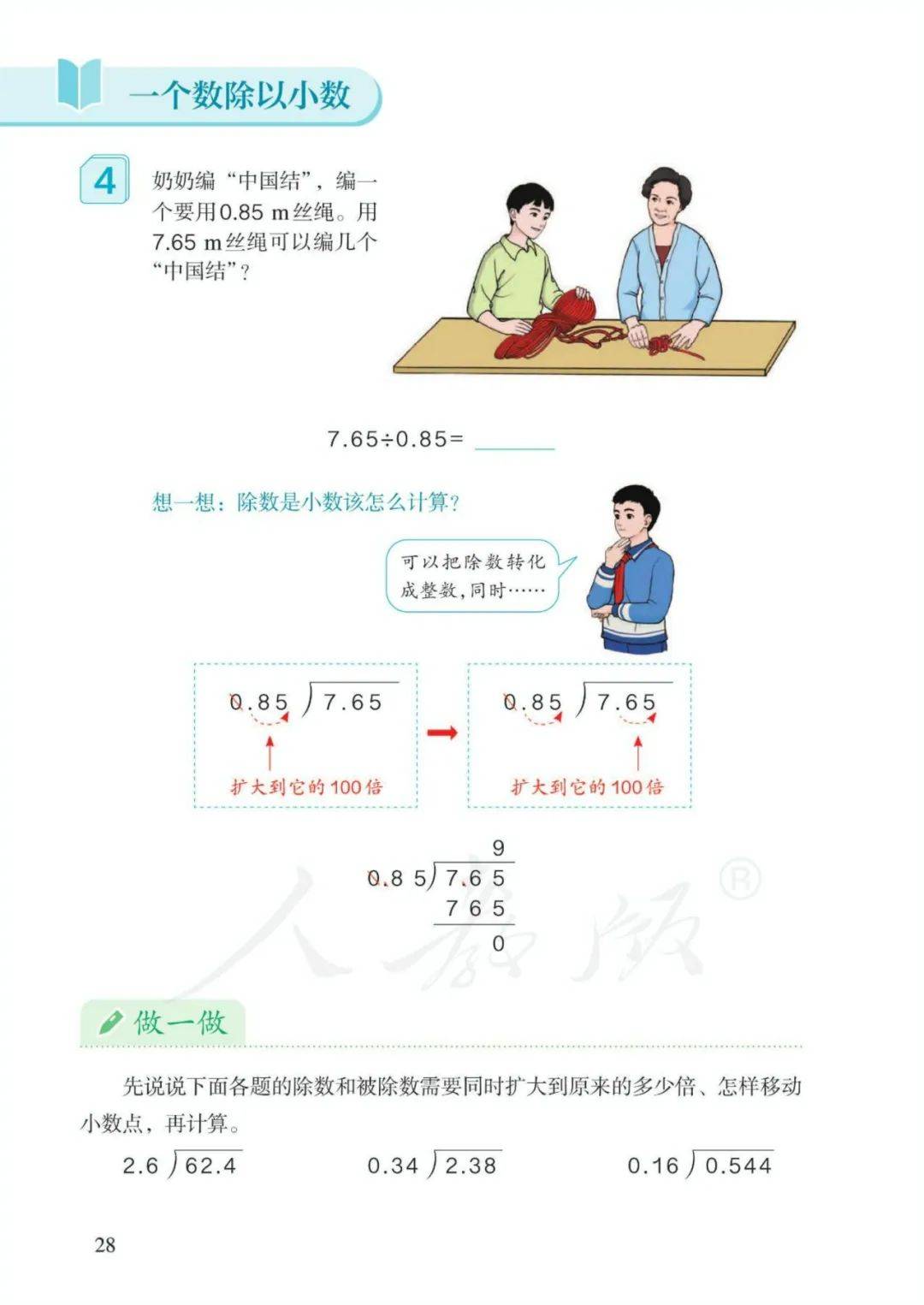
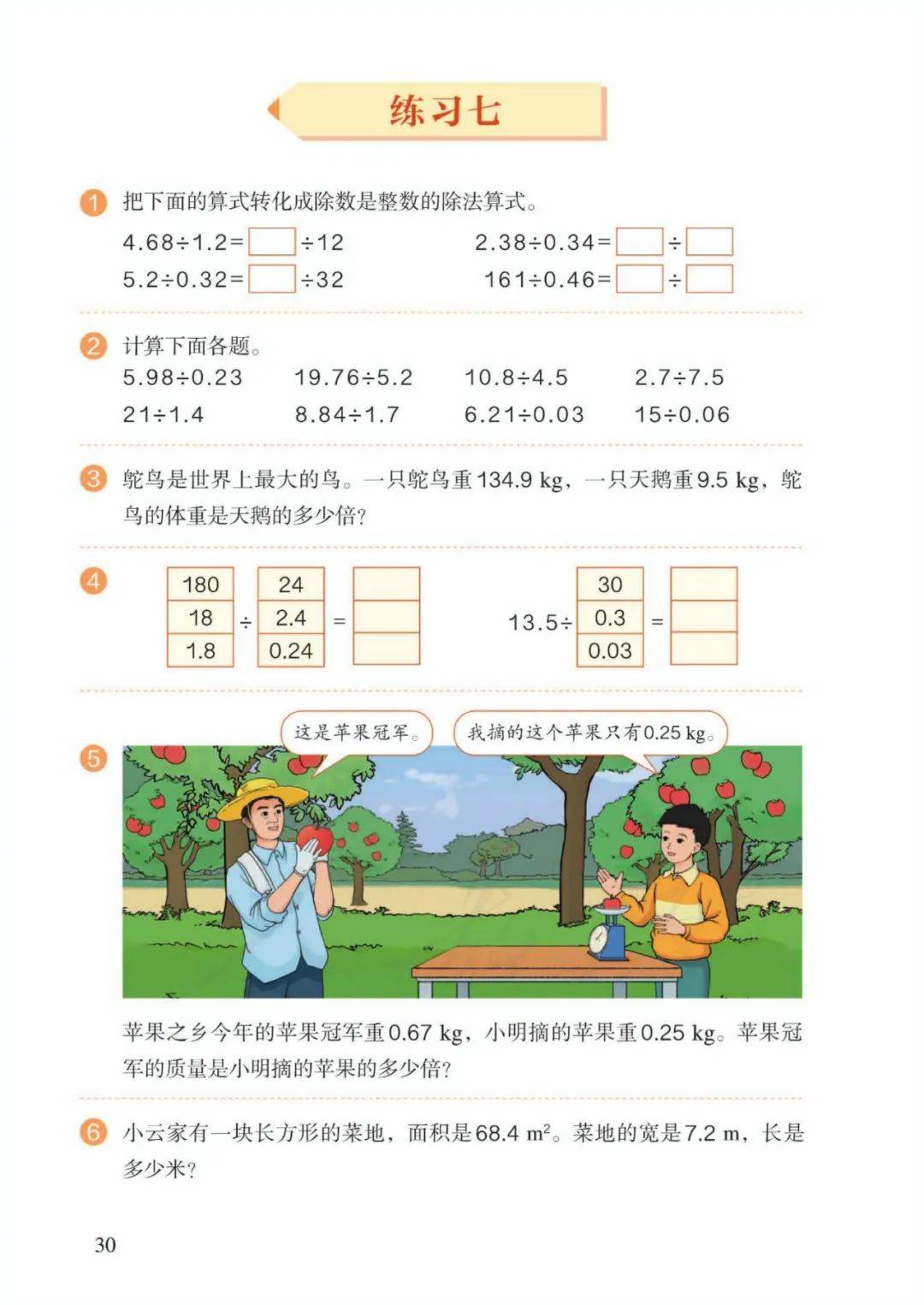
3、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。注意:如果被除数的位数不够,在被除数的末尾用0补足。
4、在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
5、除法中的变化规律:①商不变:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。②除数不变,被除数扩大,商随着扩大。③被除数不变,除数缩小,商扩大。
6、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫作循环小数。循环节:一个循环小数的小数部分,依次不断重复出现的数字。如6.3232……的循环节是32.
7、小数部分的位数是有限的小数,叫作有限小数。小数部分的位数是无限的小数,叫作无限小数。
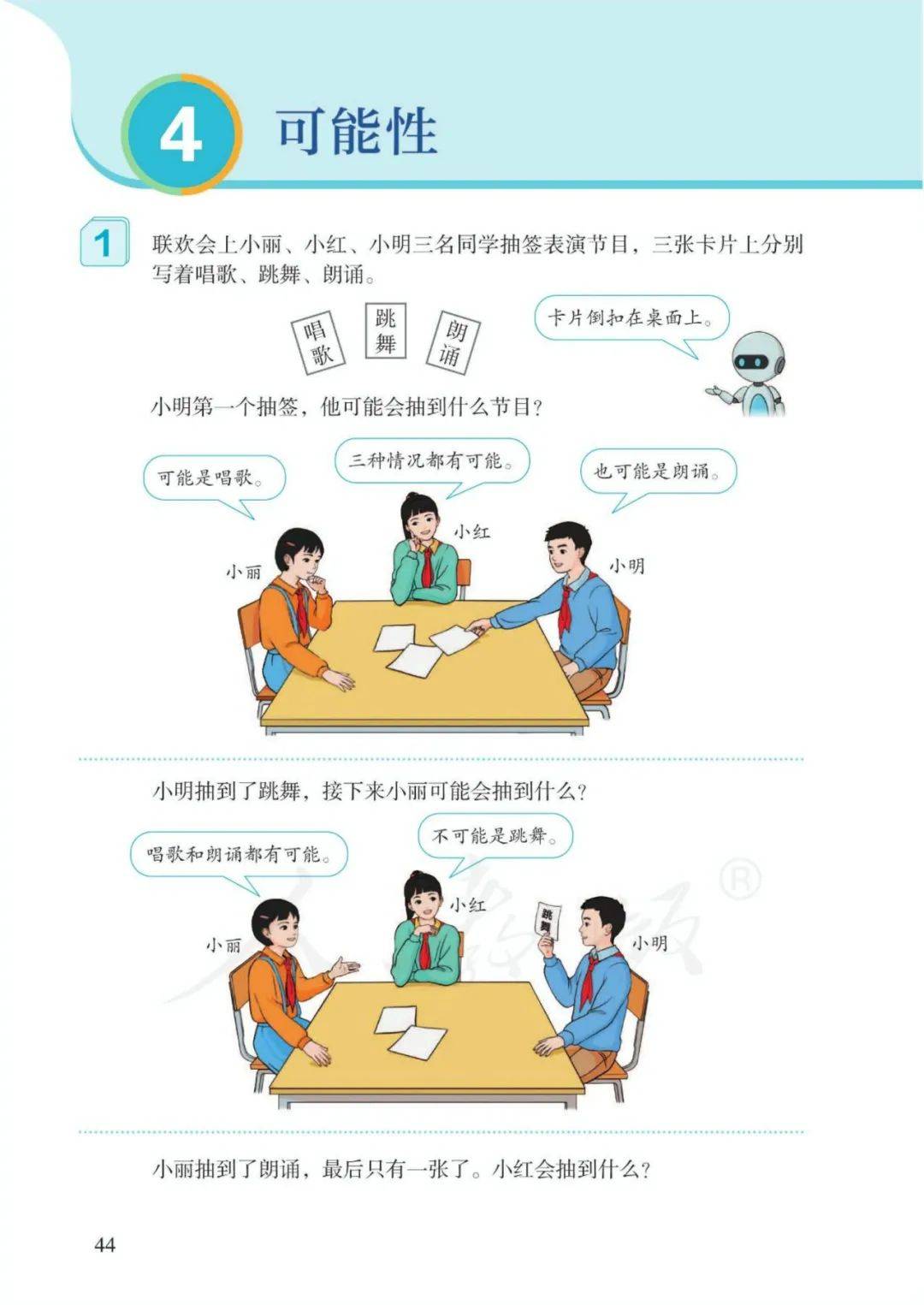
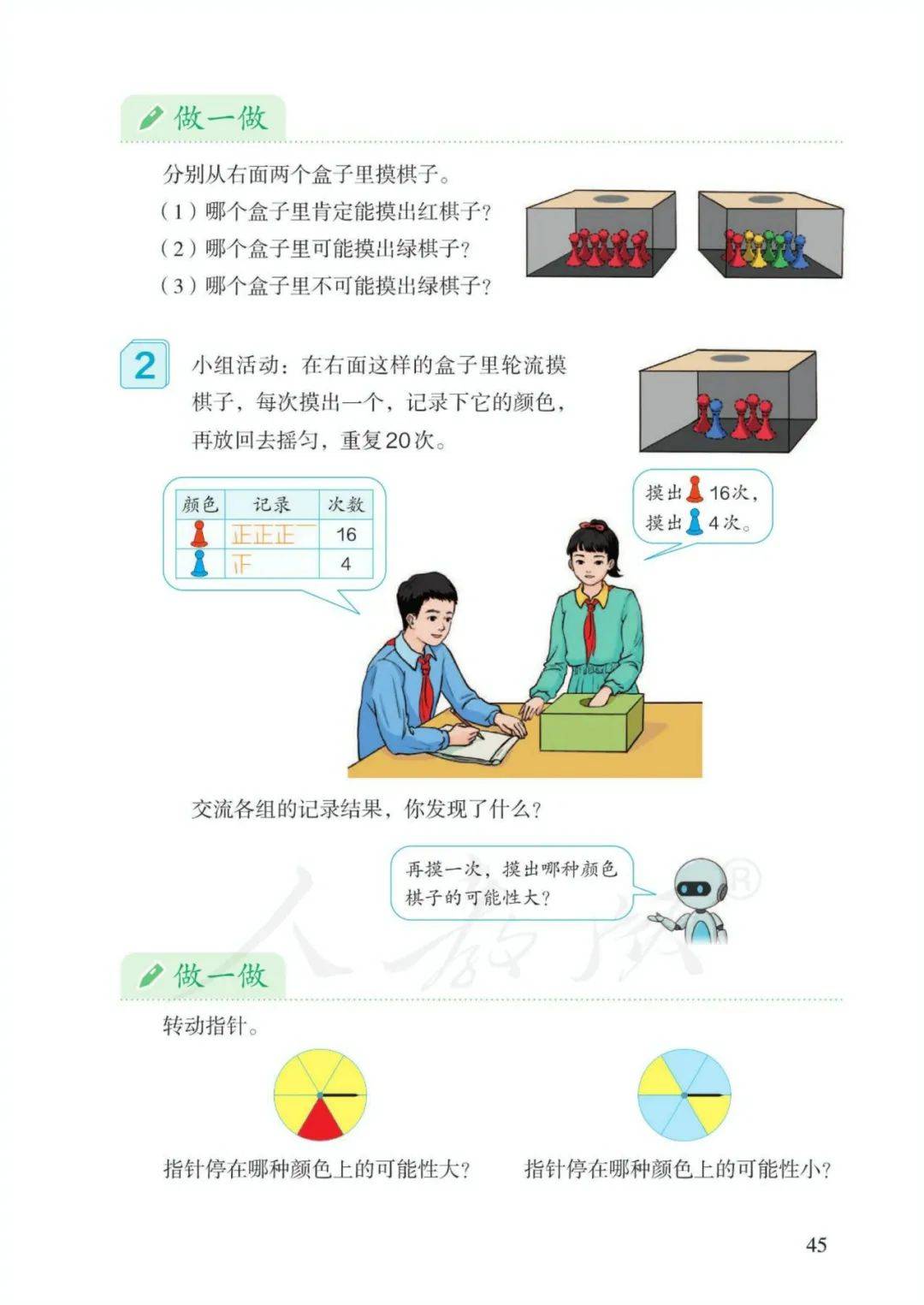
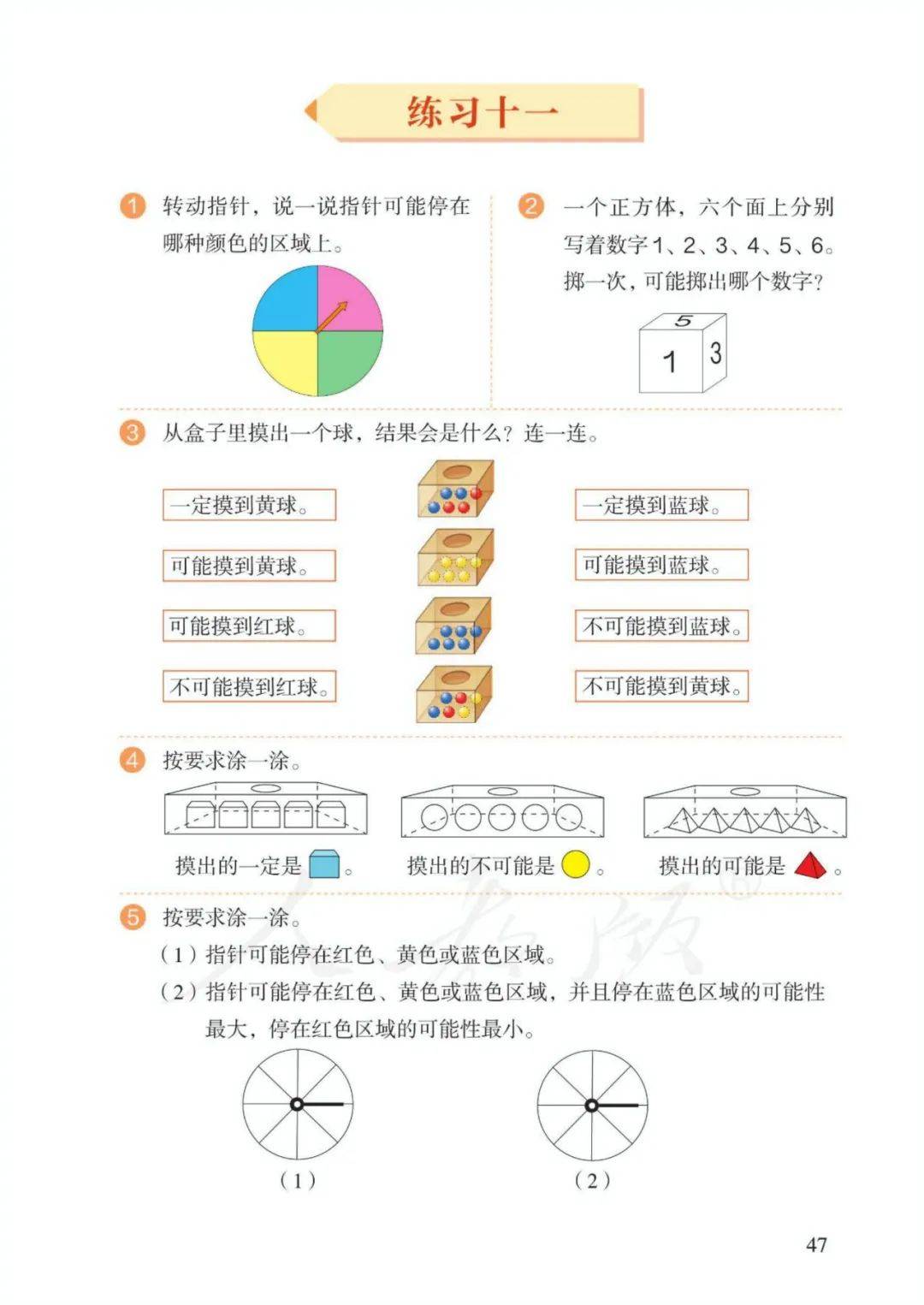
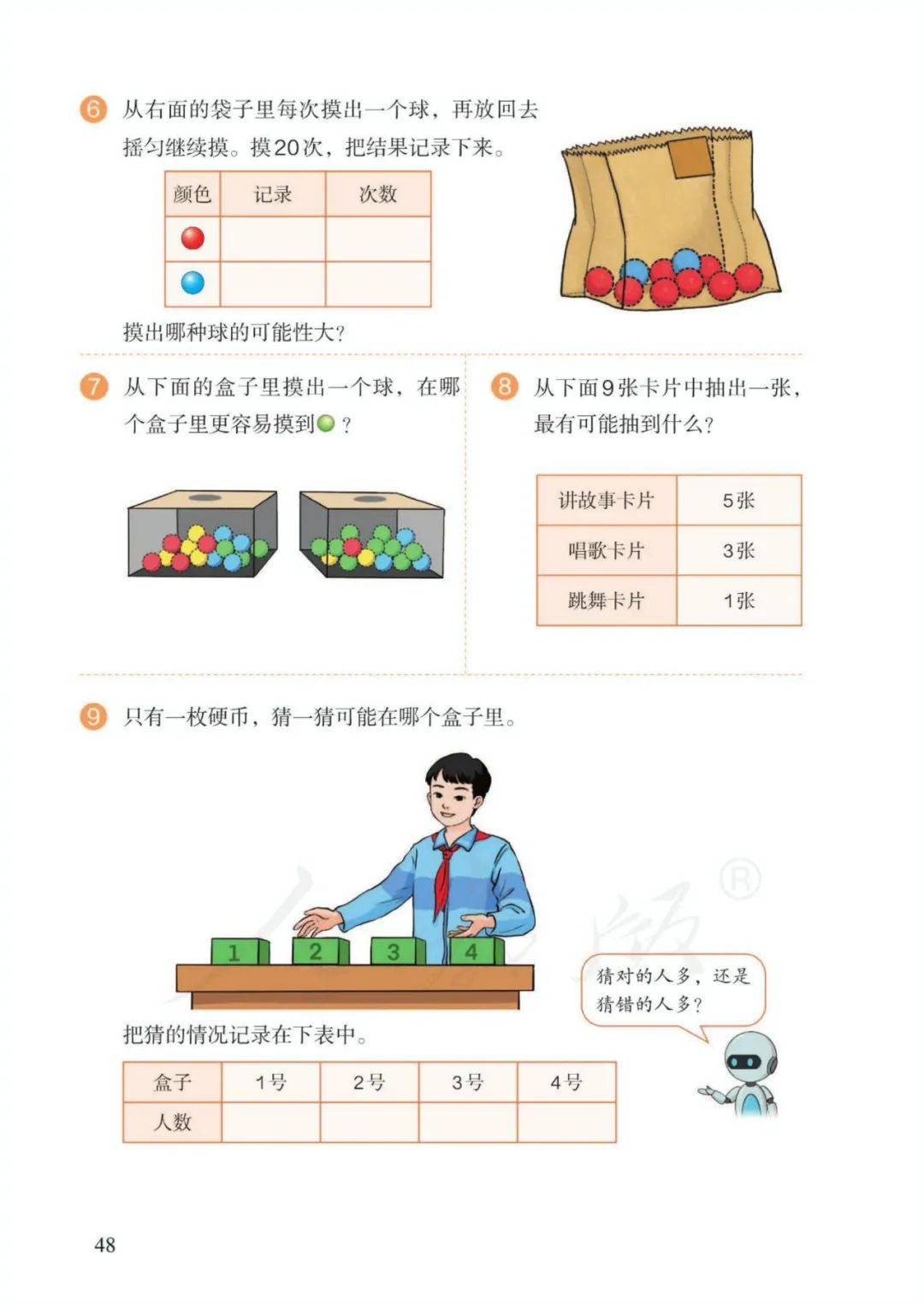
第四单元 可能性
1、有些事件的发生是确定的,有些是不确定的。

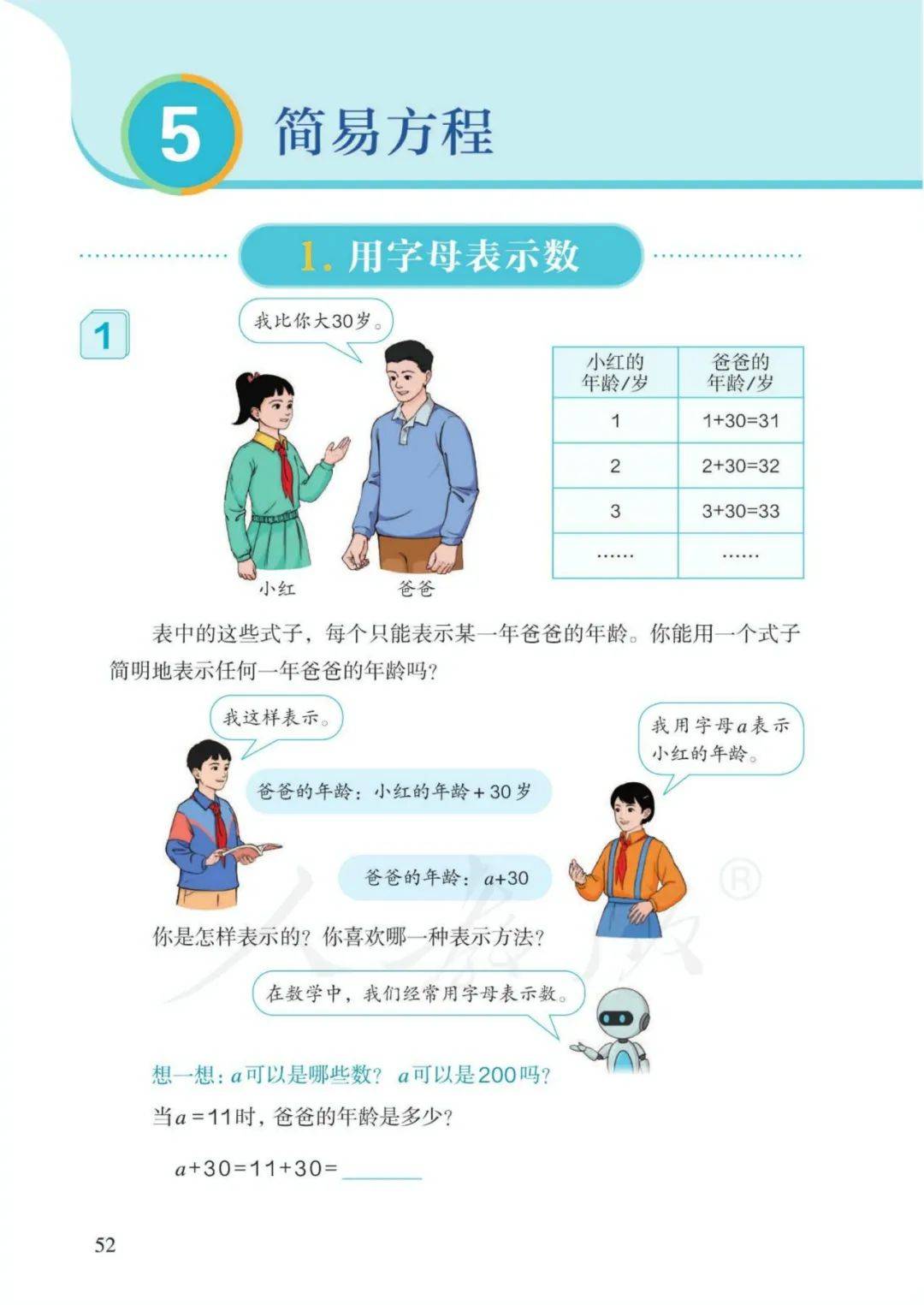
第五单元 简易方程
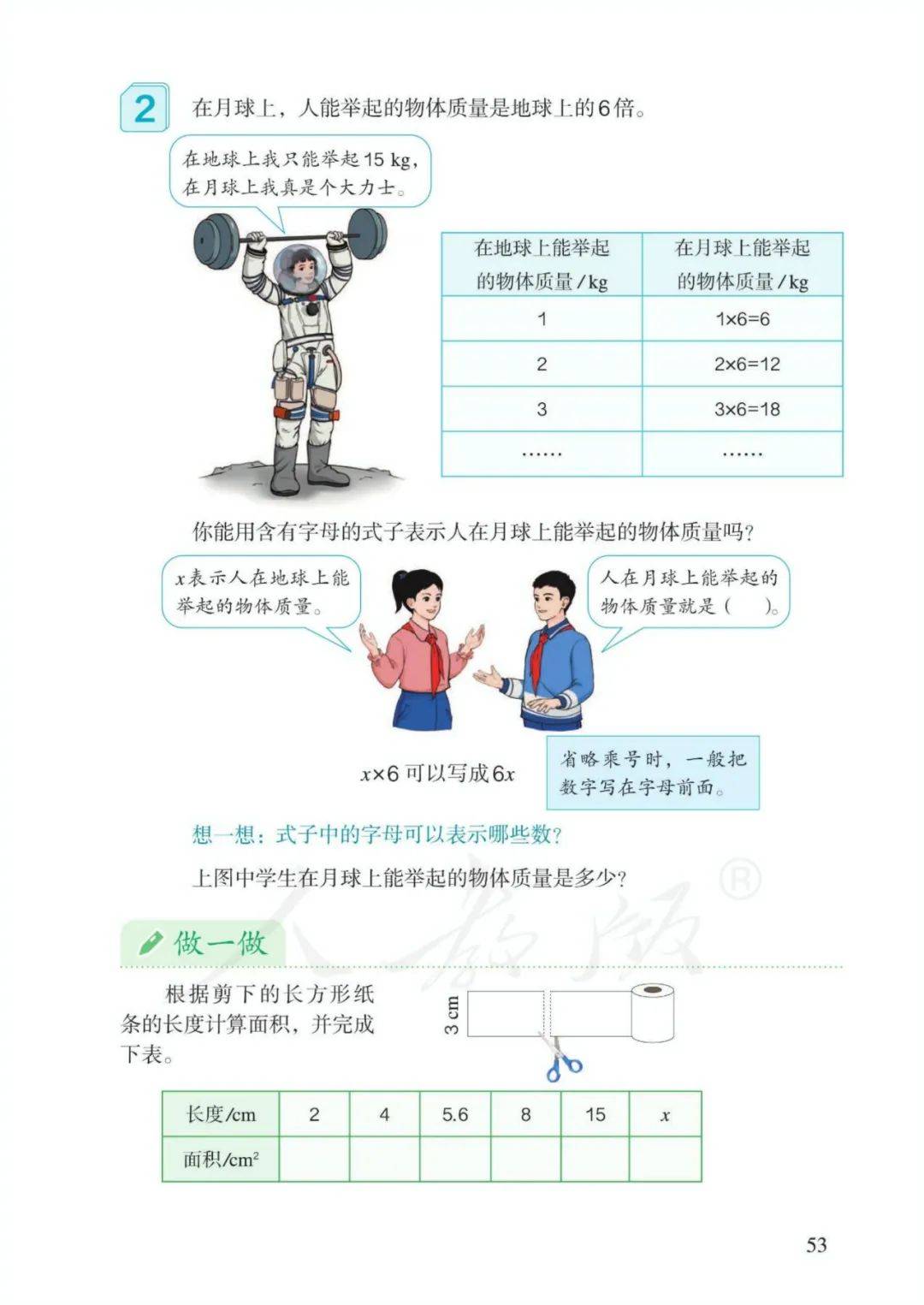
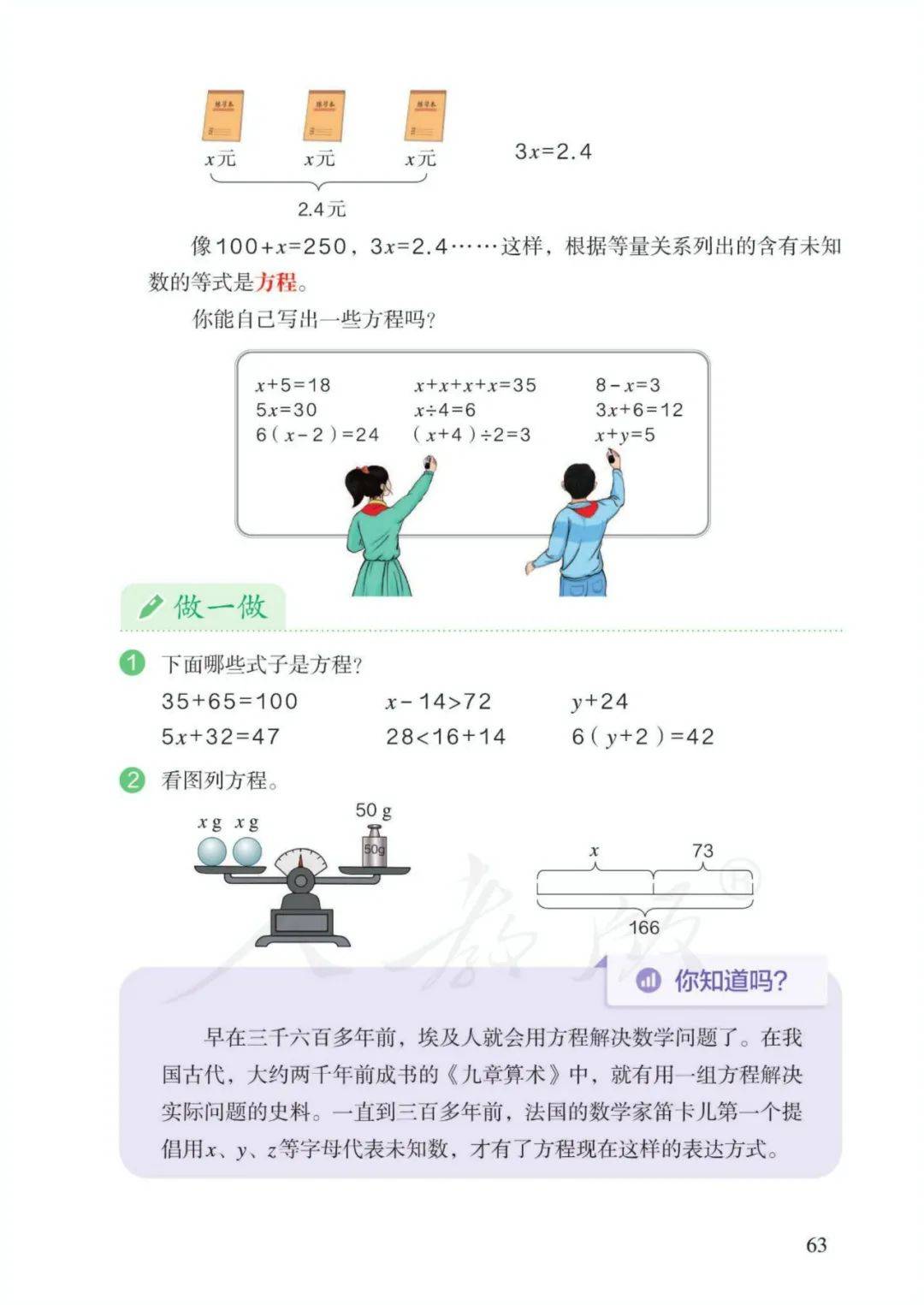
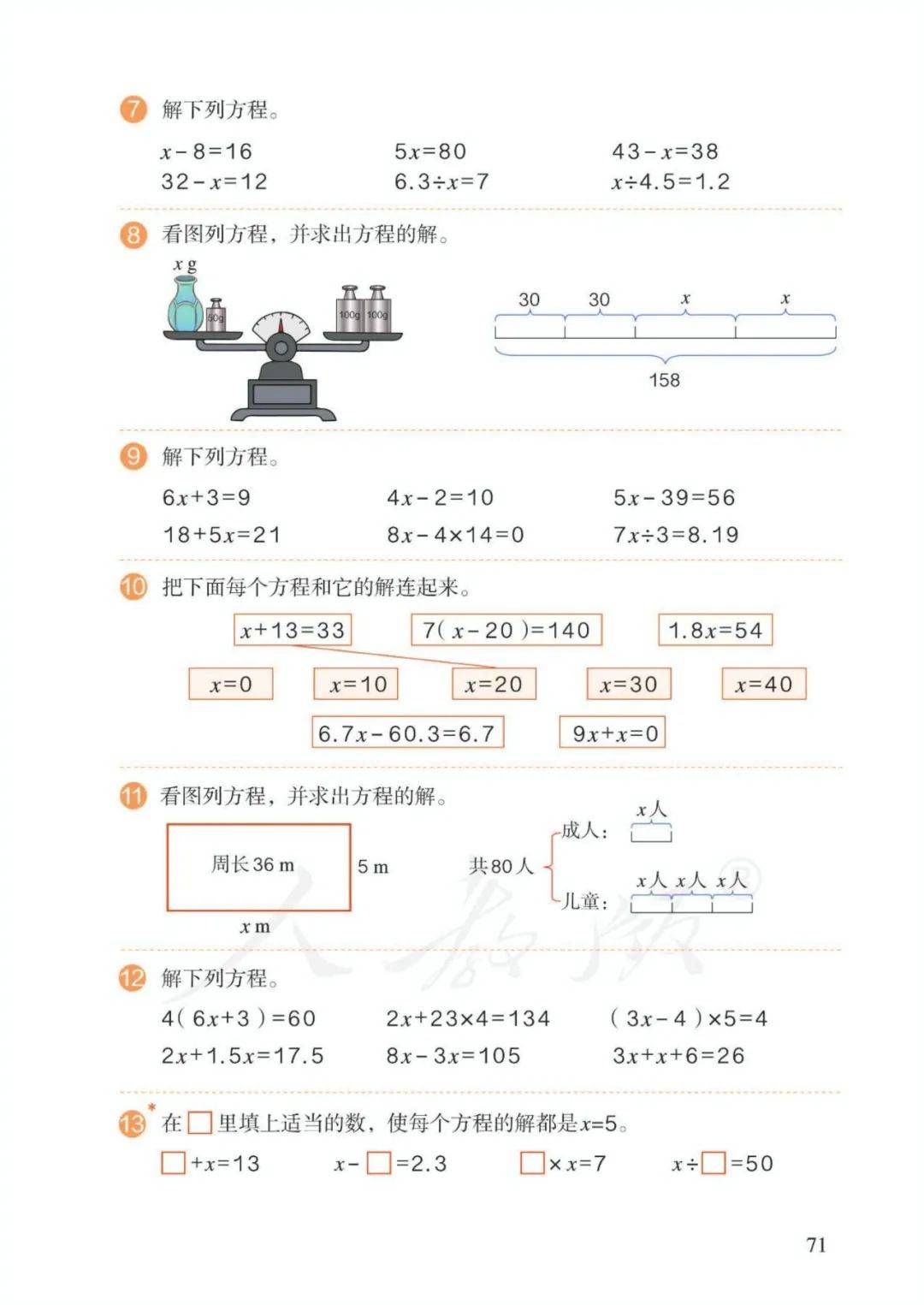
1、在含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。注: 加号、减号、除号以及数与数之间的乘号不能省略。
2、a×a可以写作a·a或a2 读作a的平方。注: 2a表示a+a ; a2表示a×a
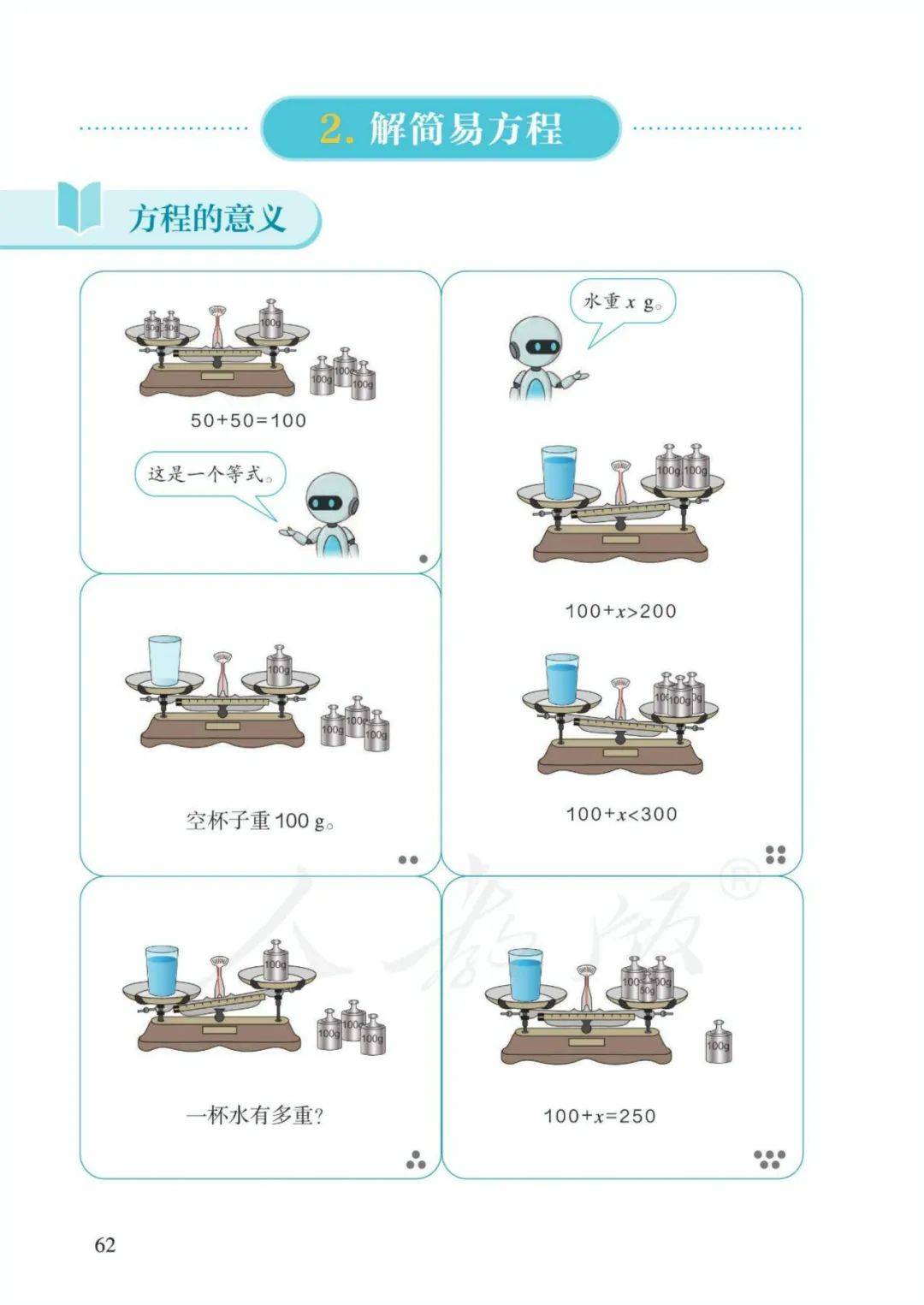
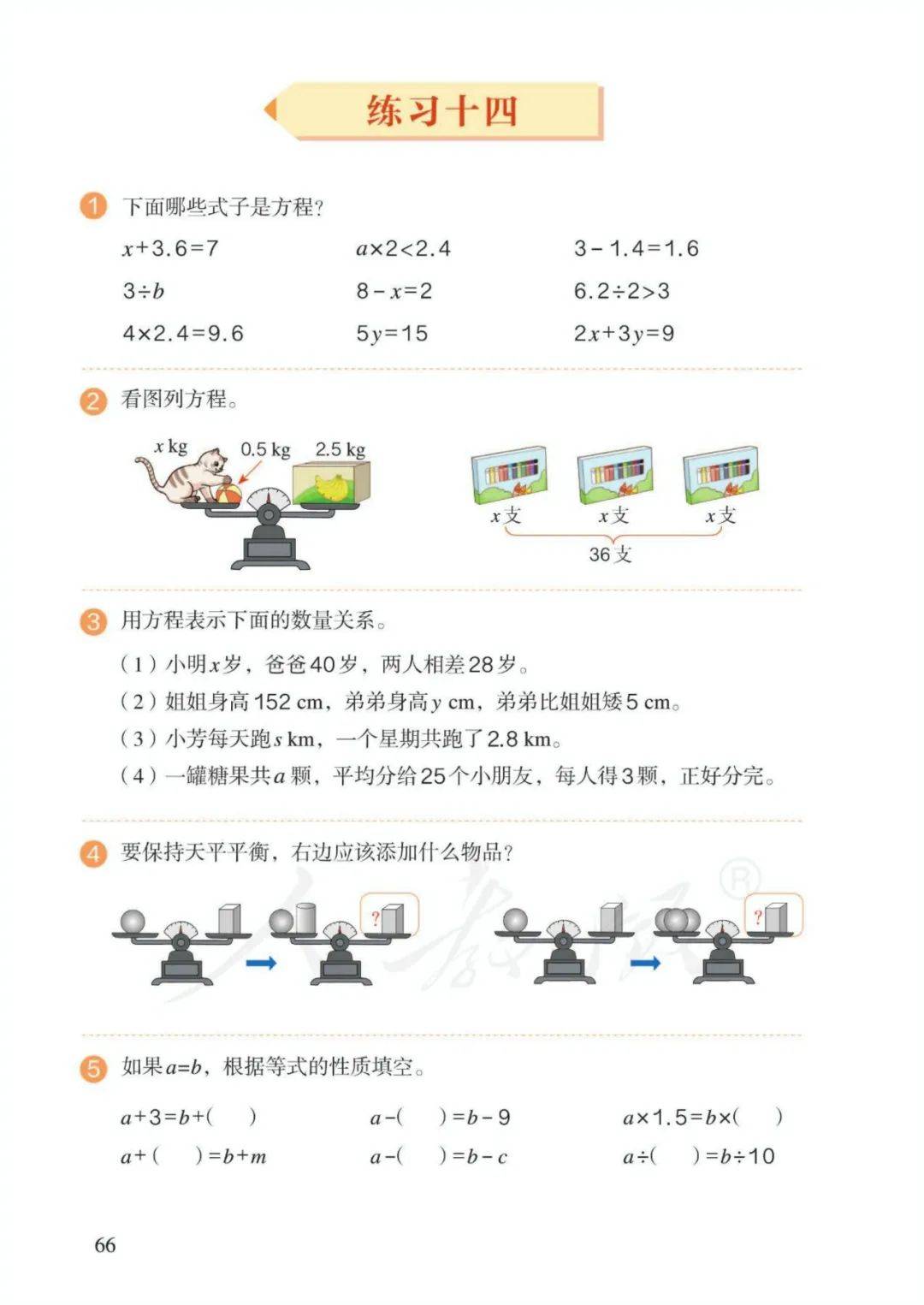
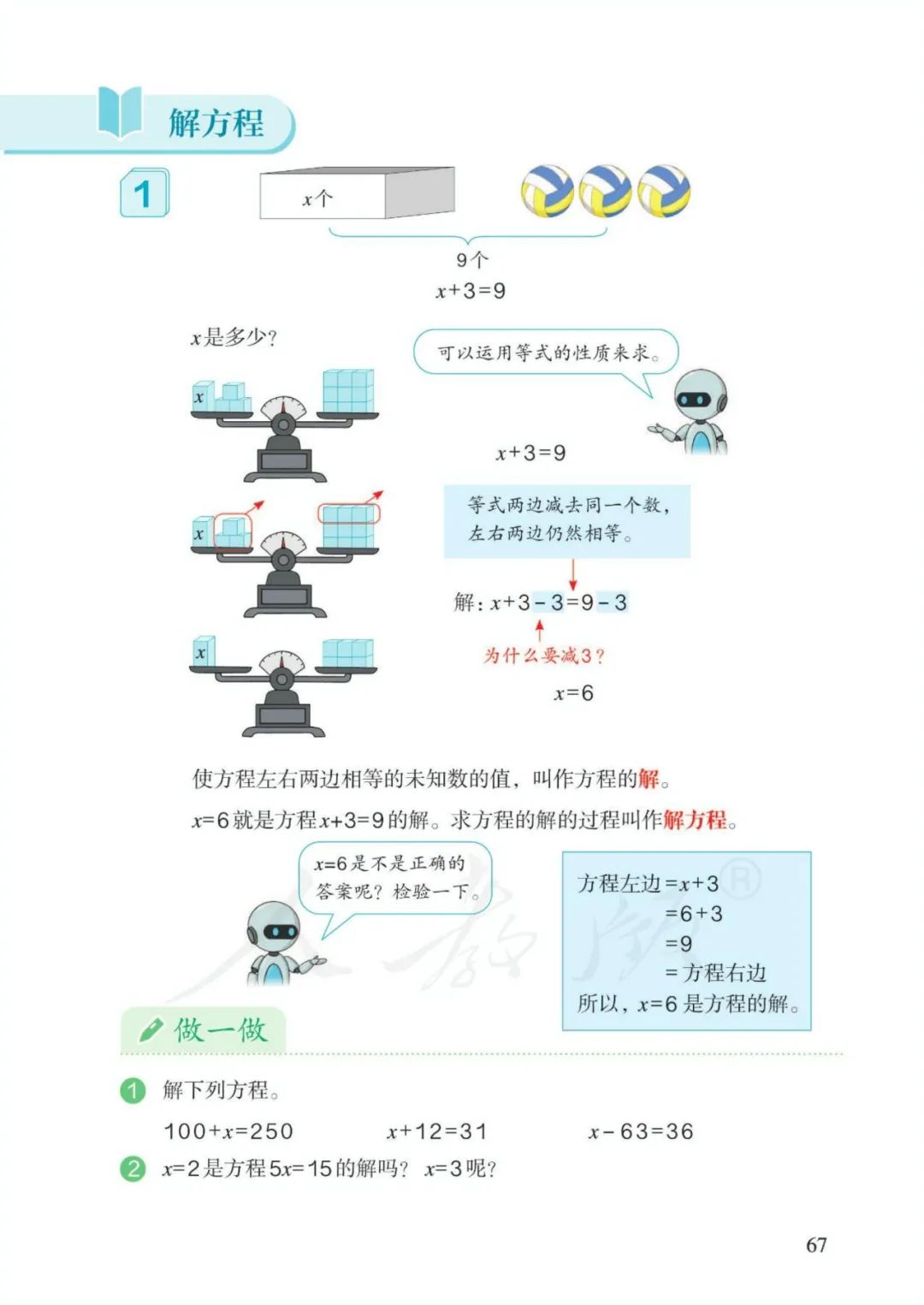
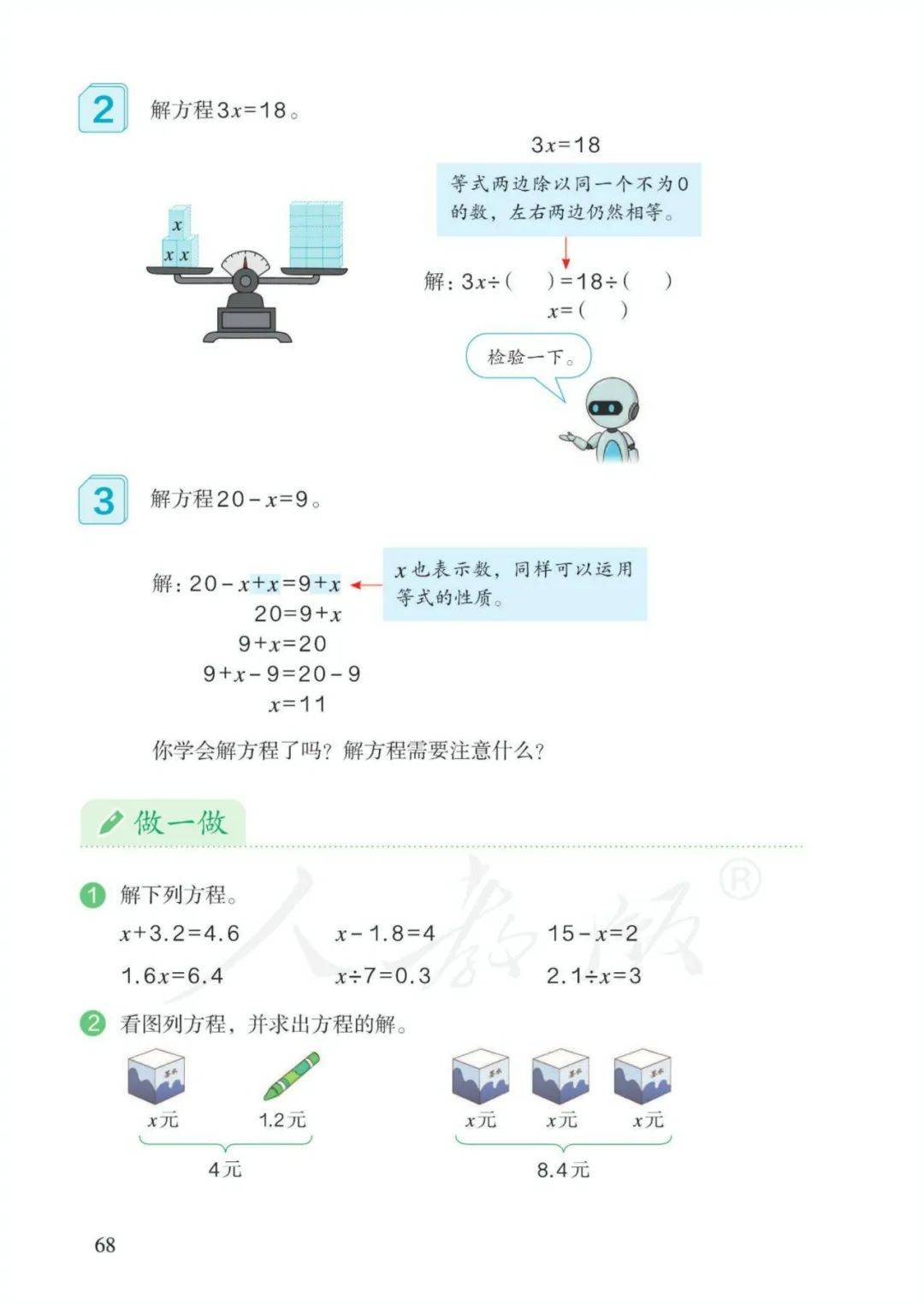
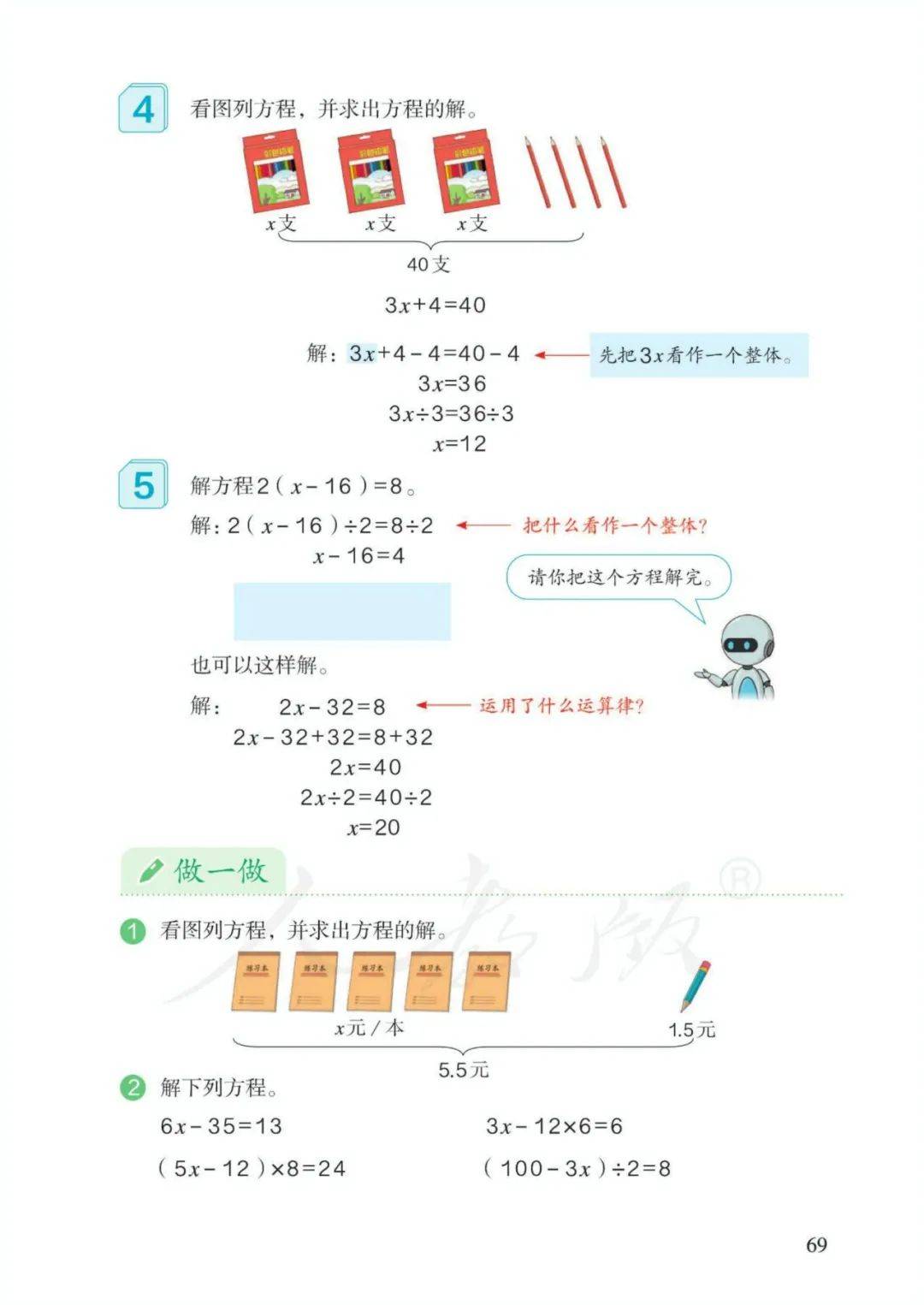
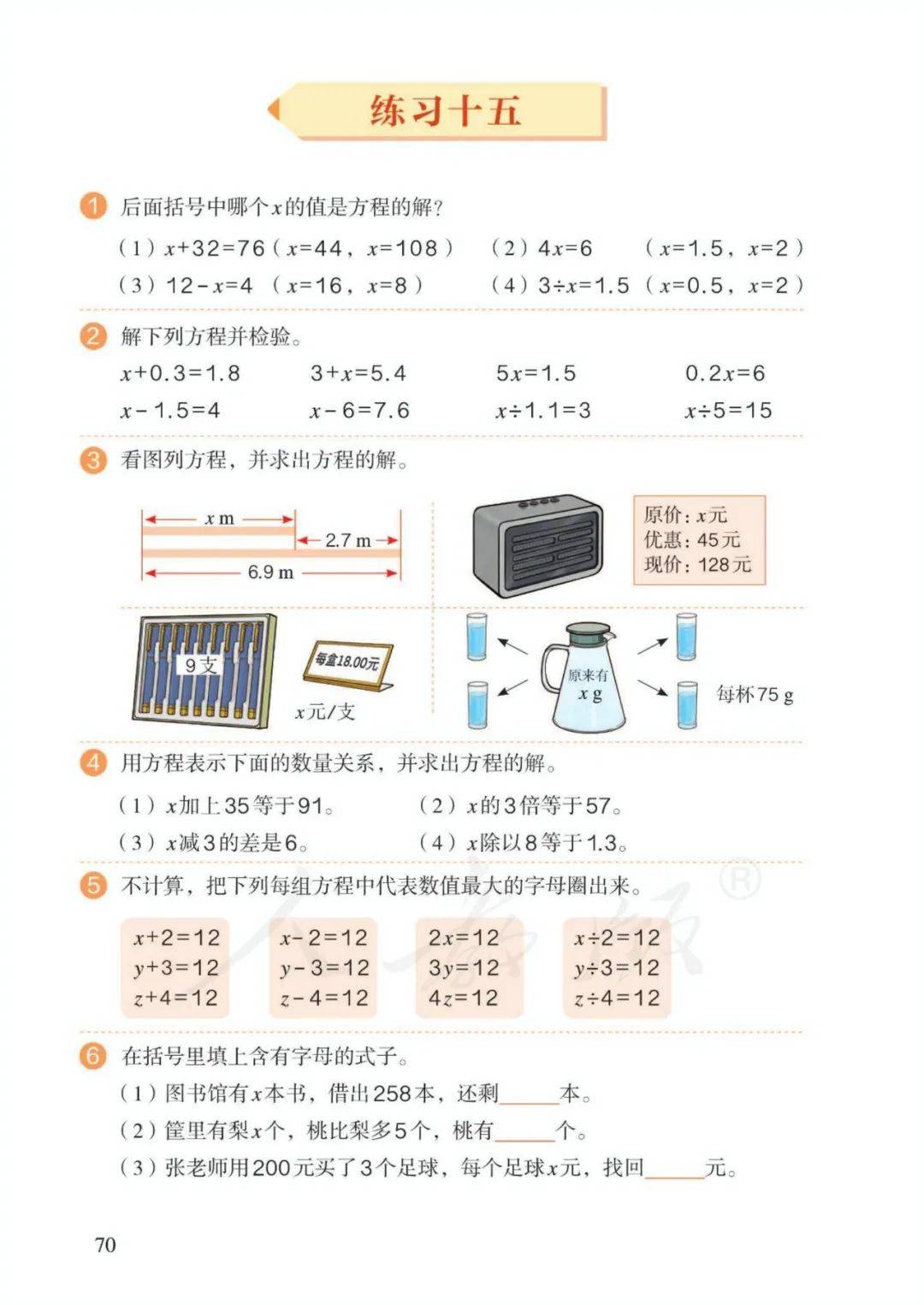
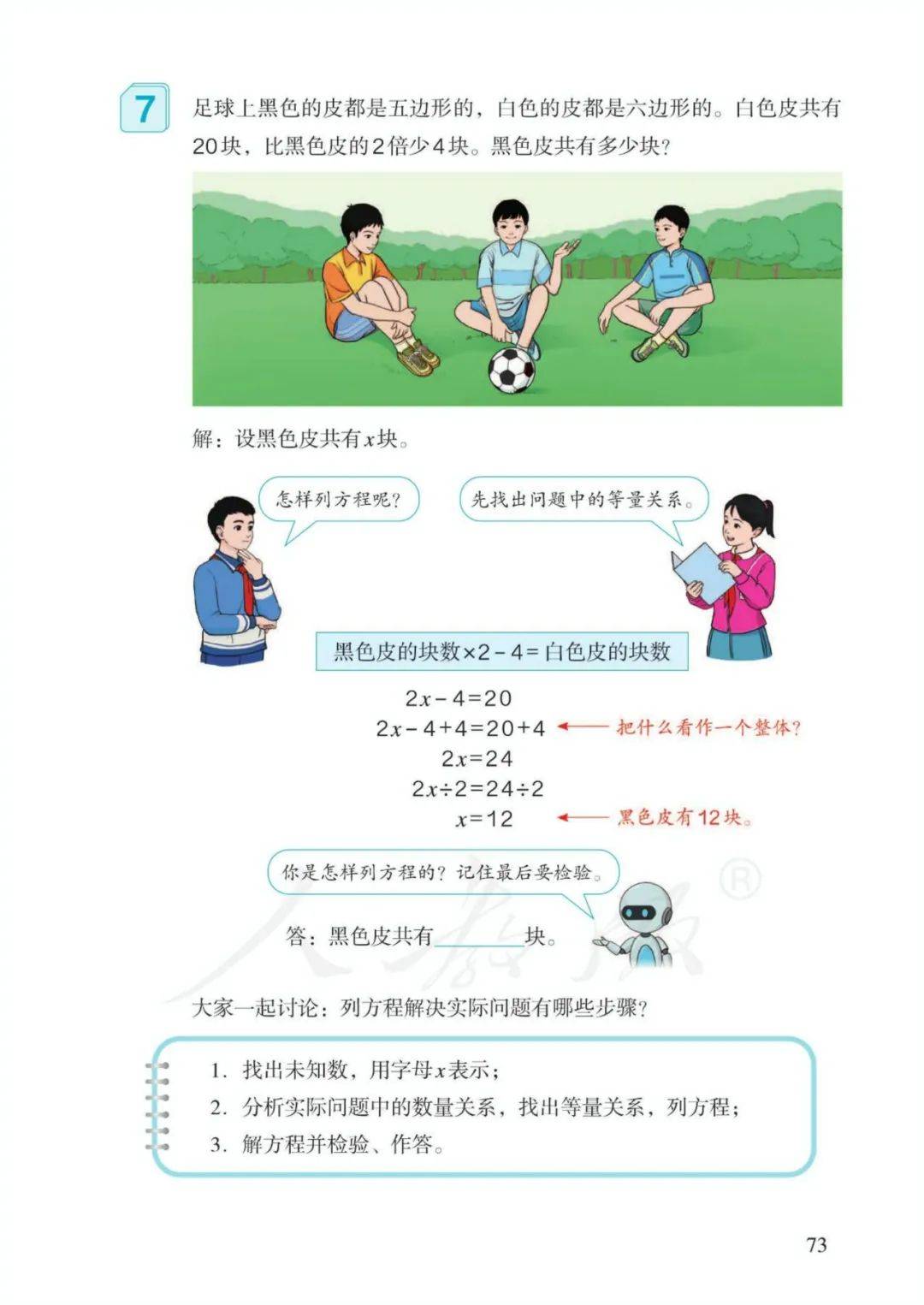
3、方程:含有未知数的等式称为方程。4、使方程左右两边相等的未知数的值,叫作方程的解。5、求方程的解的过程叫作解方程。
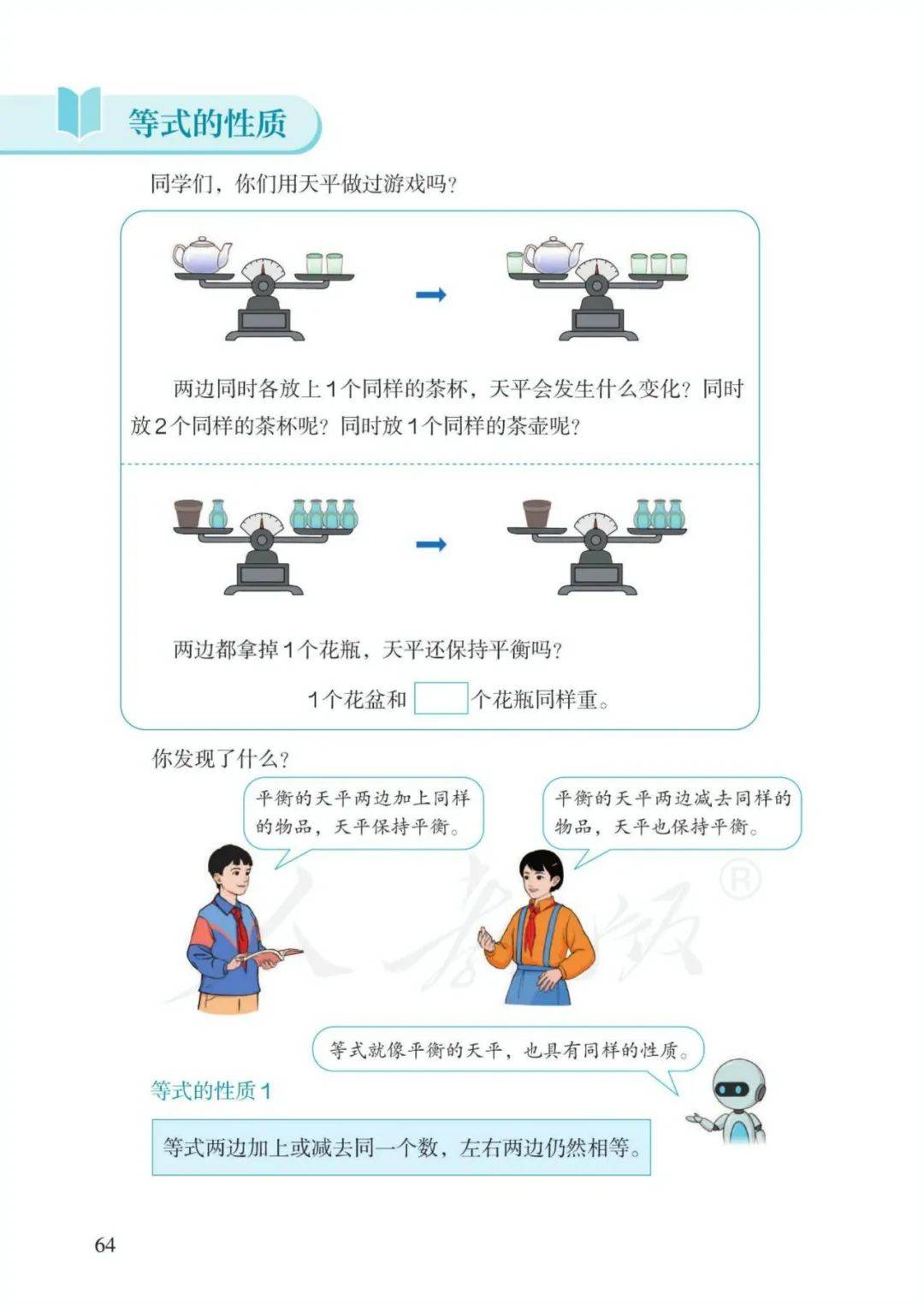
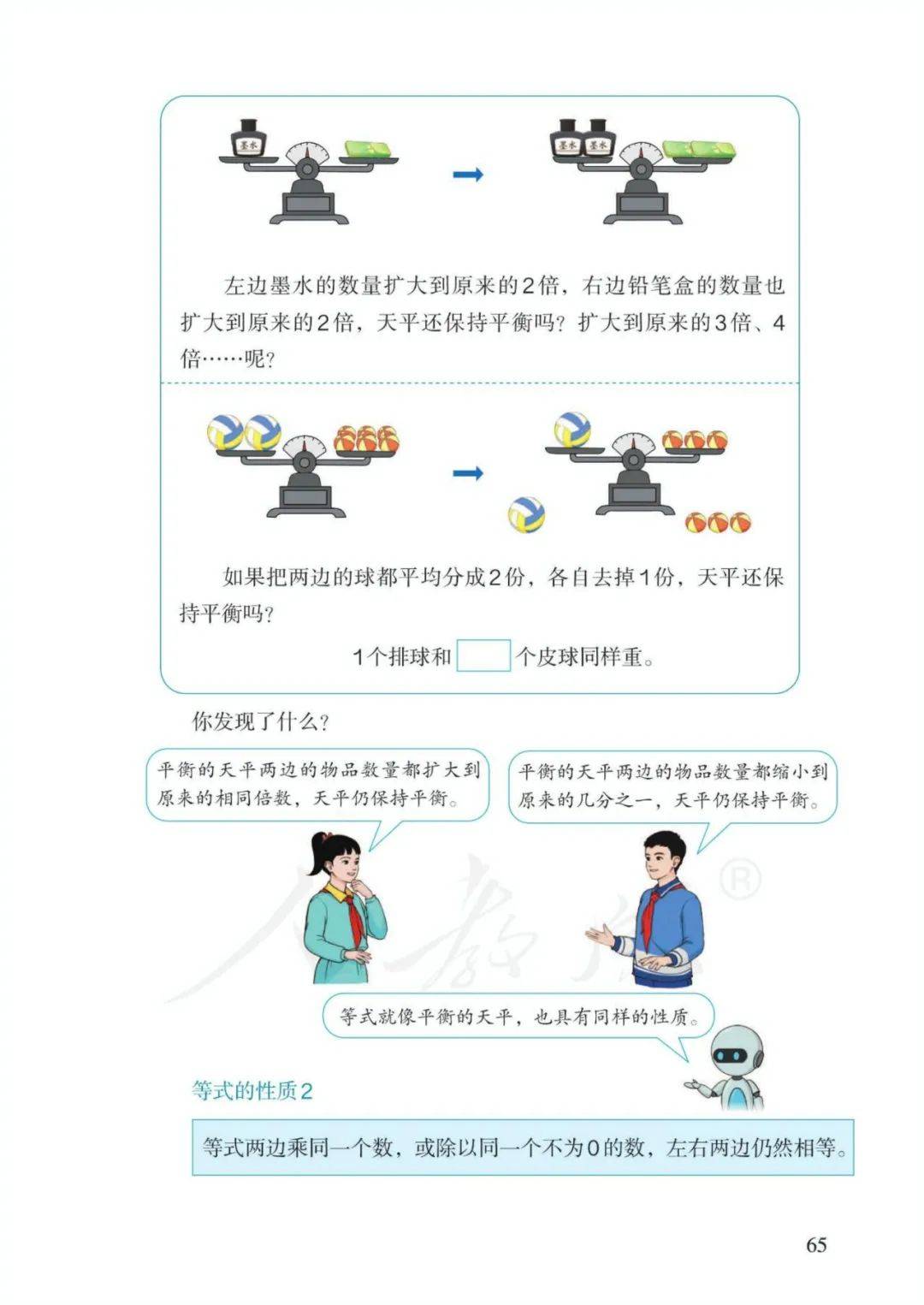
6、解方程原理:天平平衡。
等式左右两边同时加、减、乘、除相同的数(0除外),等式依然成立。
7、10个数量关系式
加法;和=加数+加数;一个加数=和-另一个加数
减法:差=被减数-减数;被减数=差+减数;减数=被减数-差
乘法:积=因数×因数;一个因数=积÷另一个因数
除法:商=被除数÷除数;被除数=商×除数;除数=被除数÷商

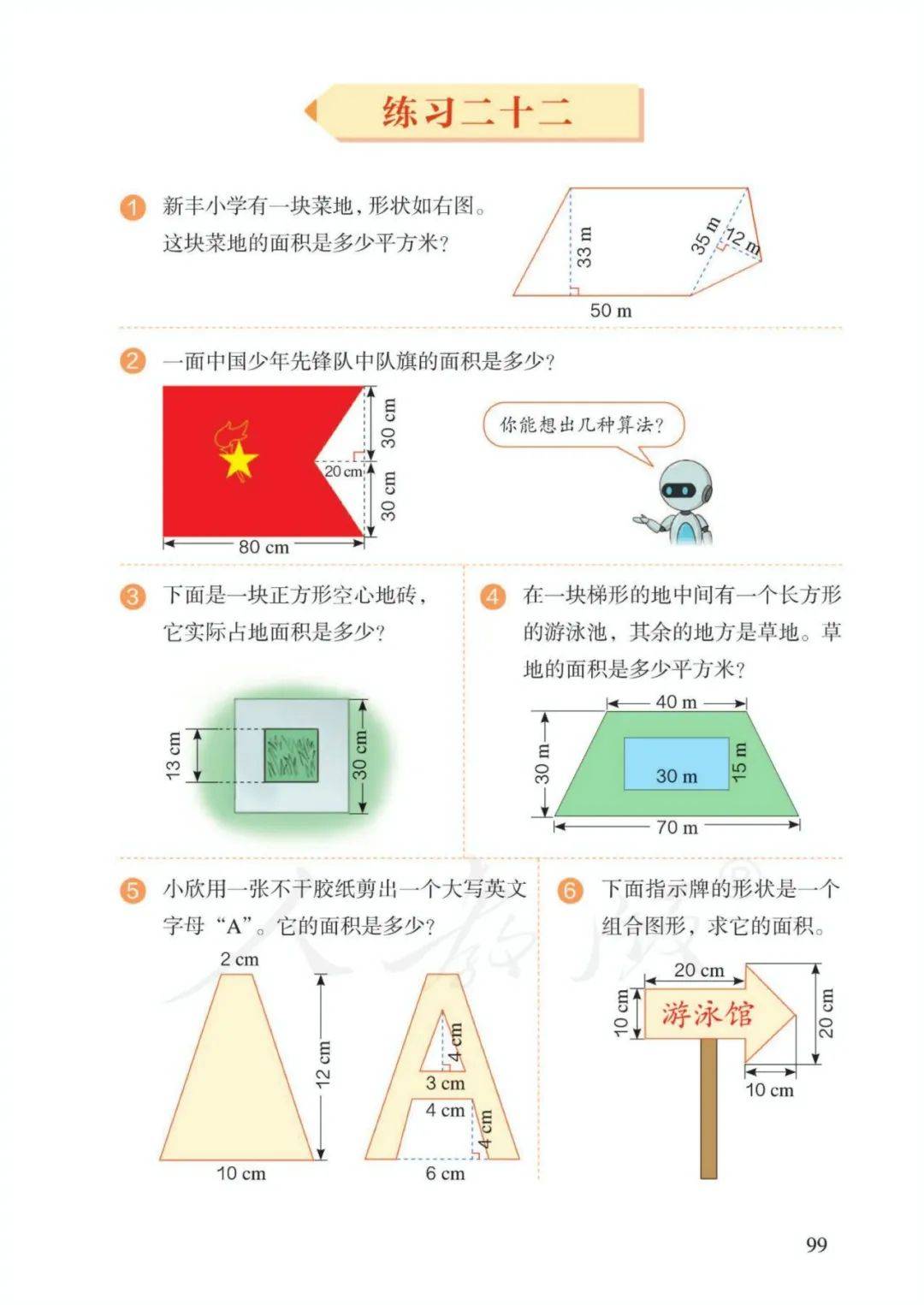
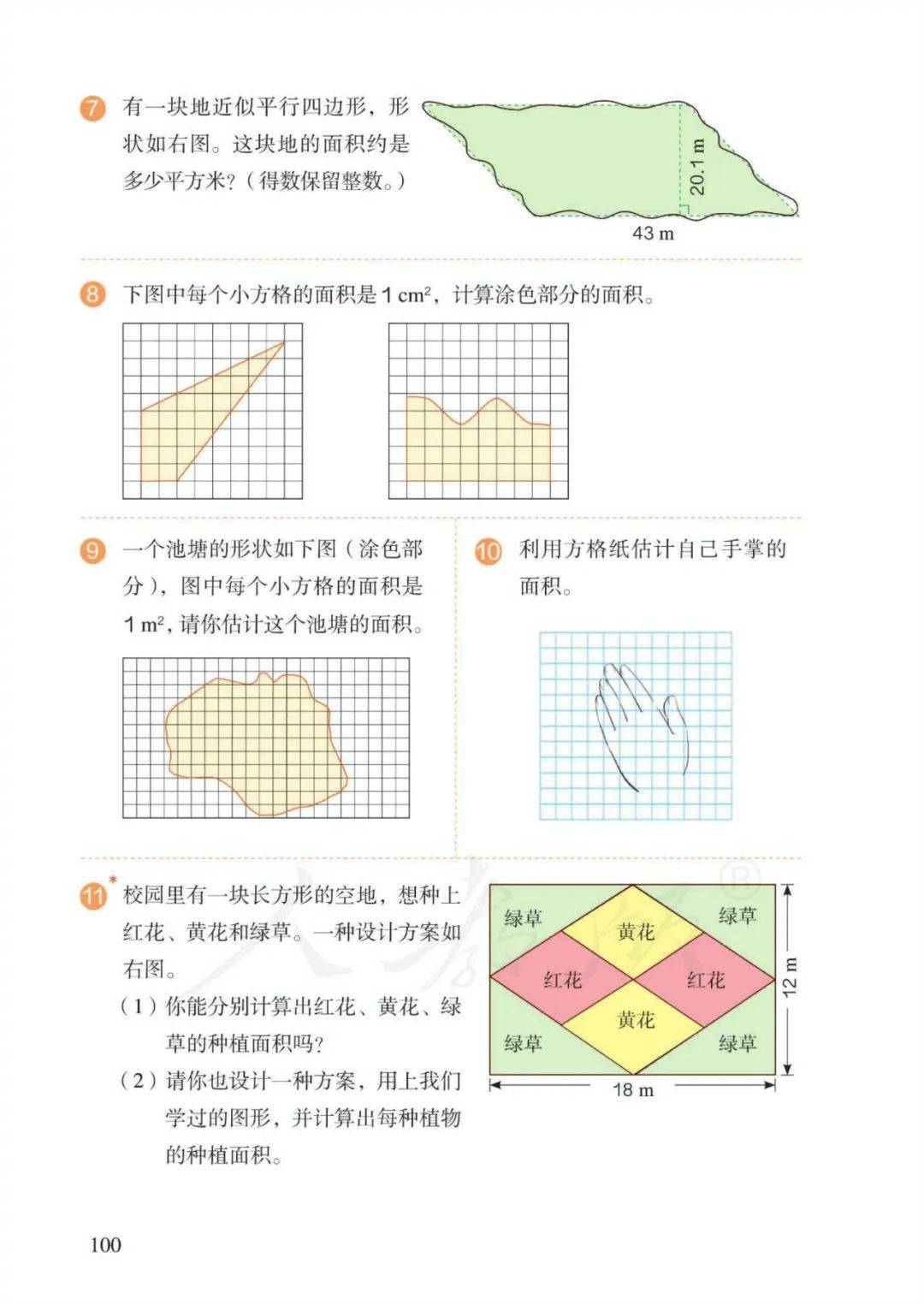
第六单元 多边形的面积
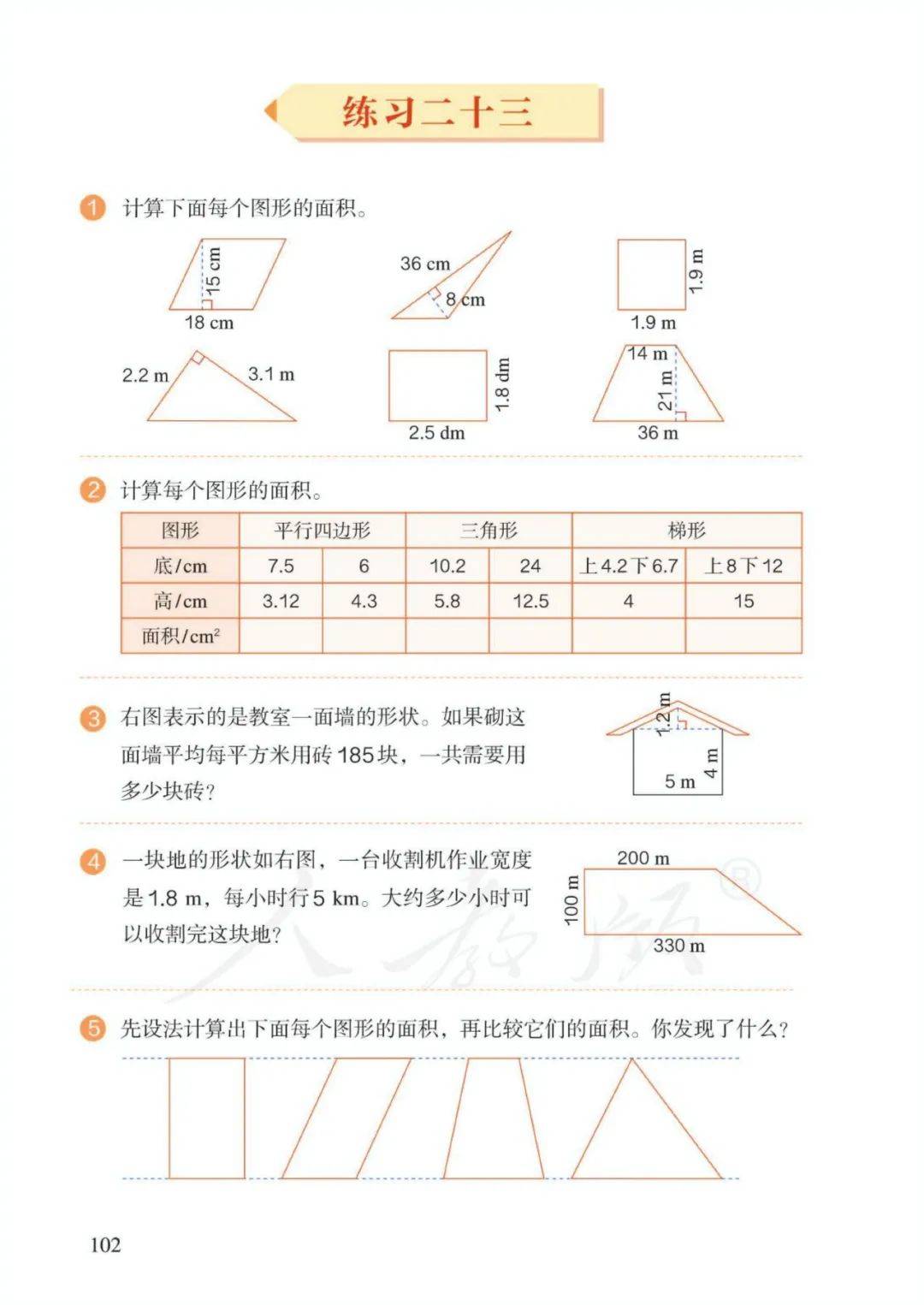
1、长方形:周长=(长+宽)×2——【长=周长÷2-宽;宽=周长÷2-长】
字母表示:C=(a+b)×2
面积=长×宽 字母表示:S=ab
2、正方形:周长=边长×4 字母表示:C=4a
面积=边长×边长 字母表示:S=a2
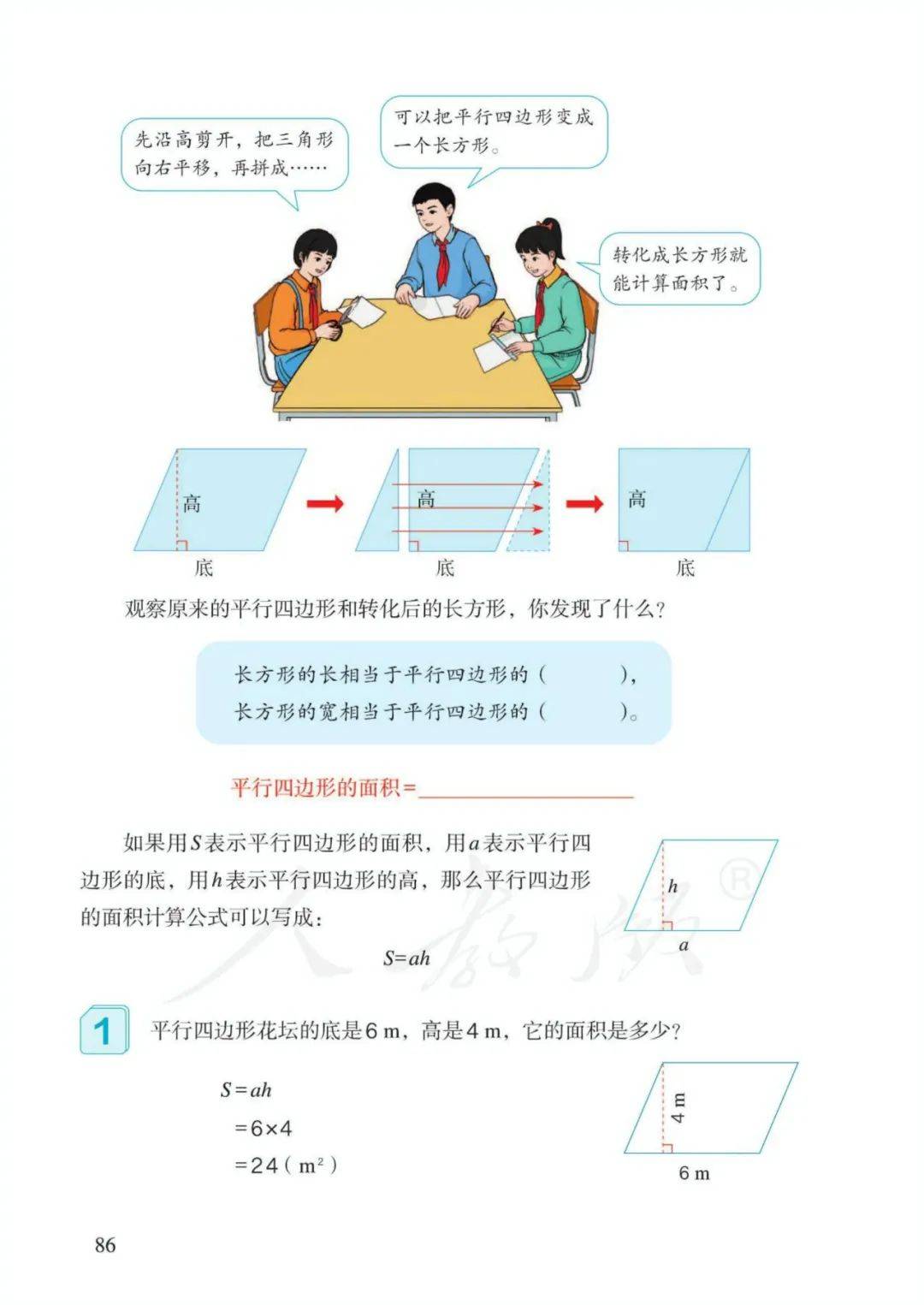
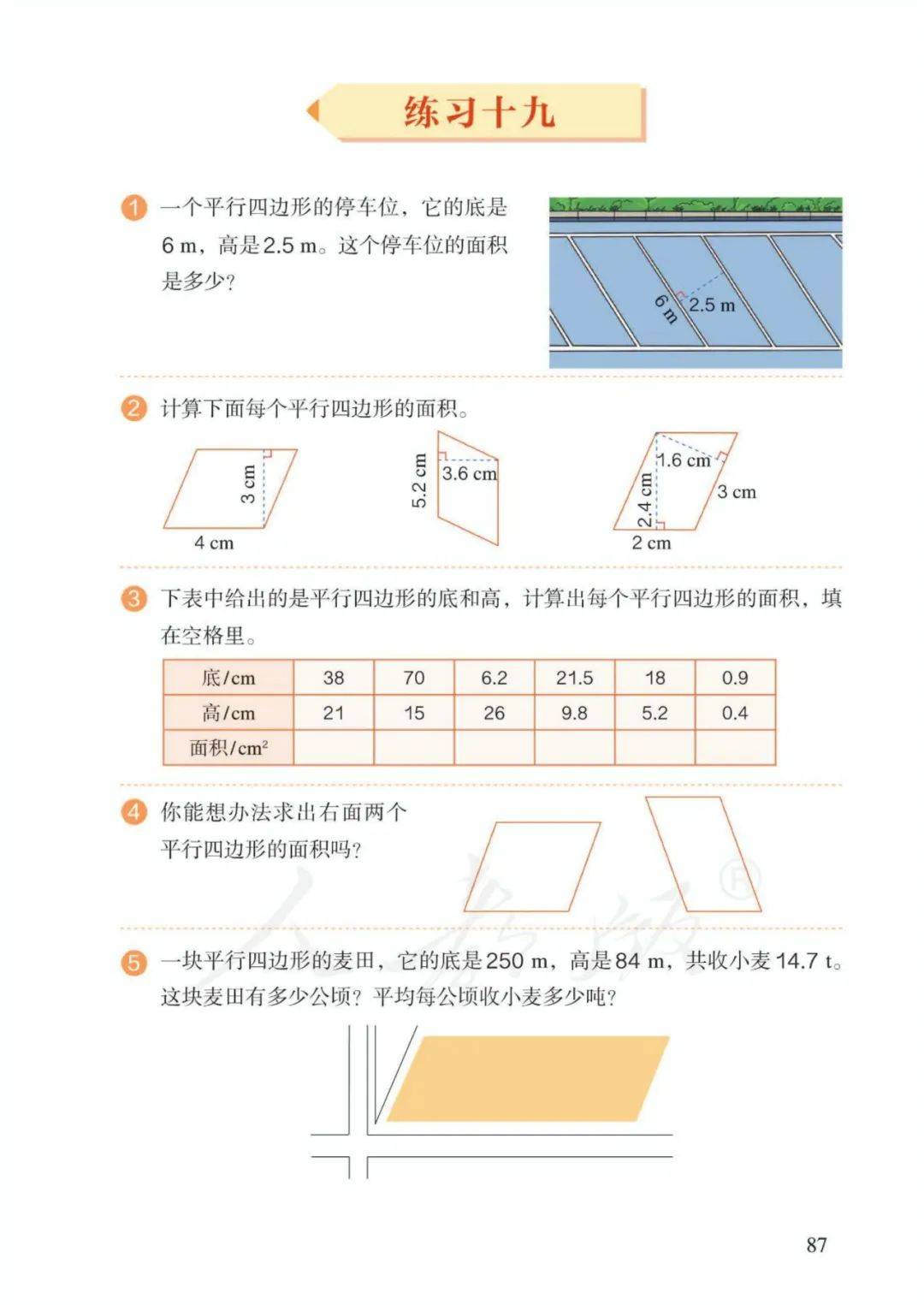
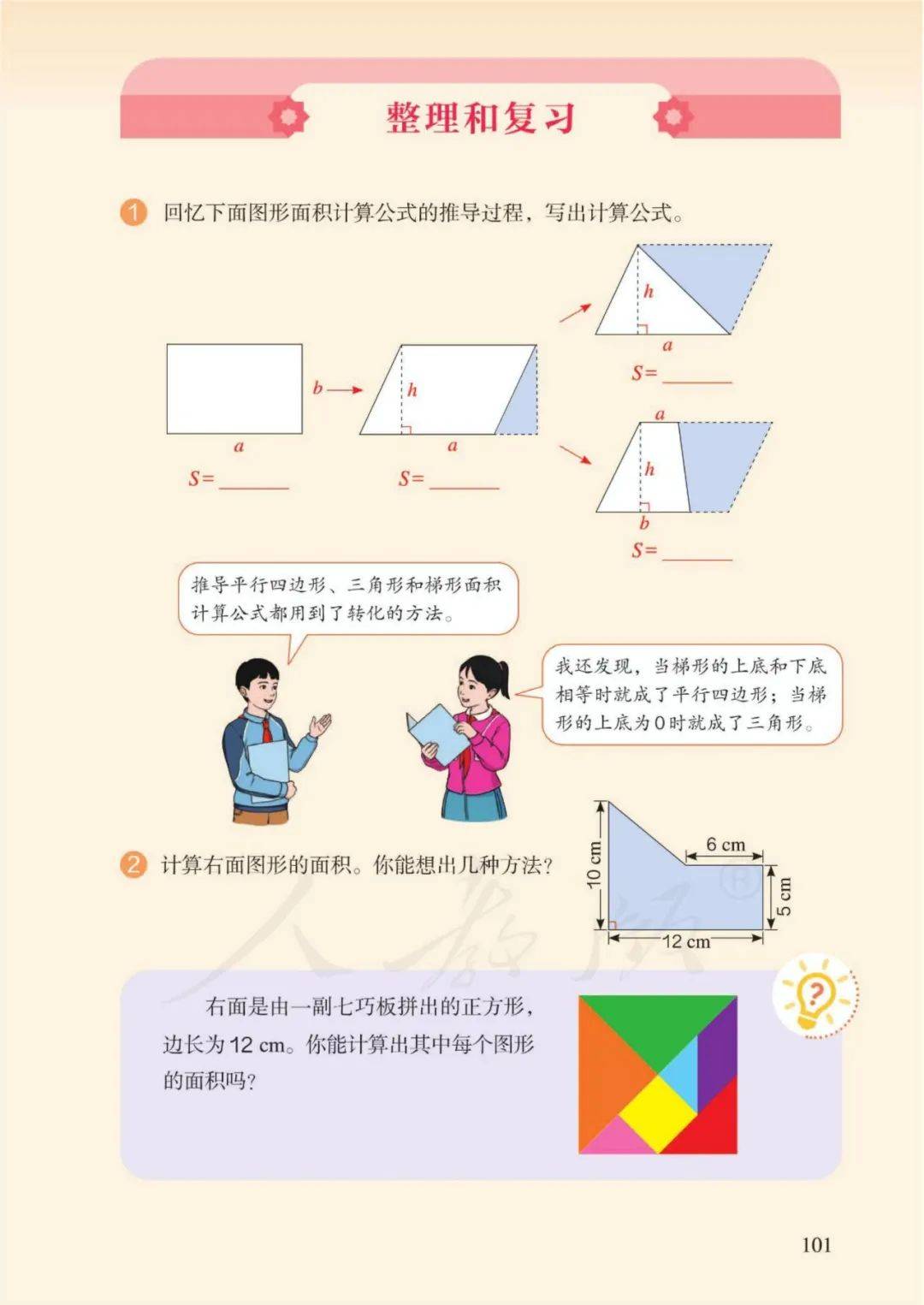
3、平行四边形的面积=底×高 字母表示: S=ah
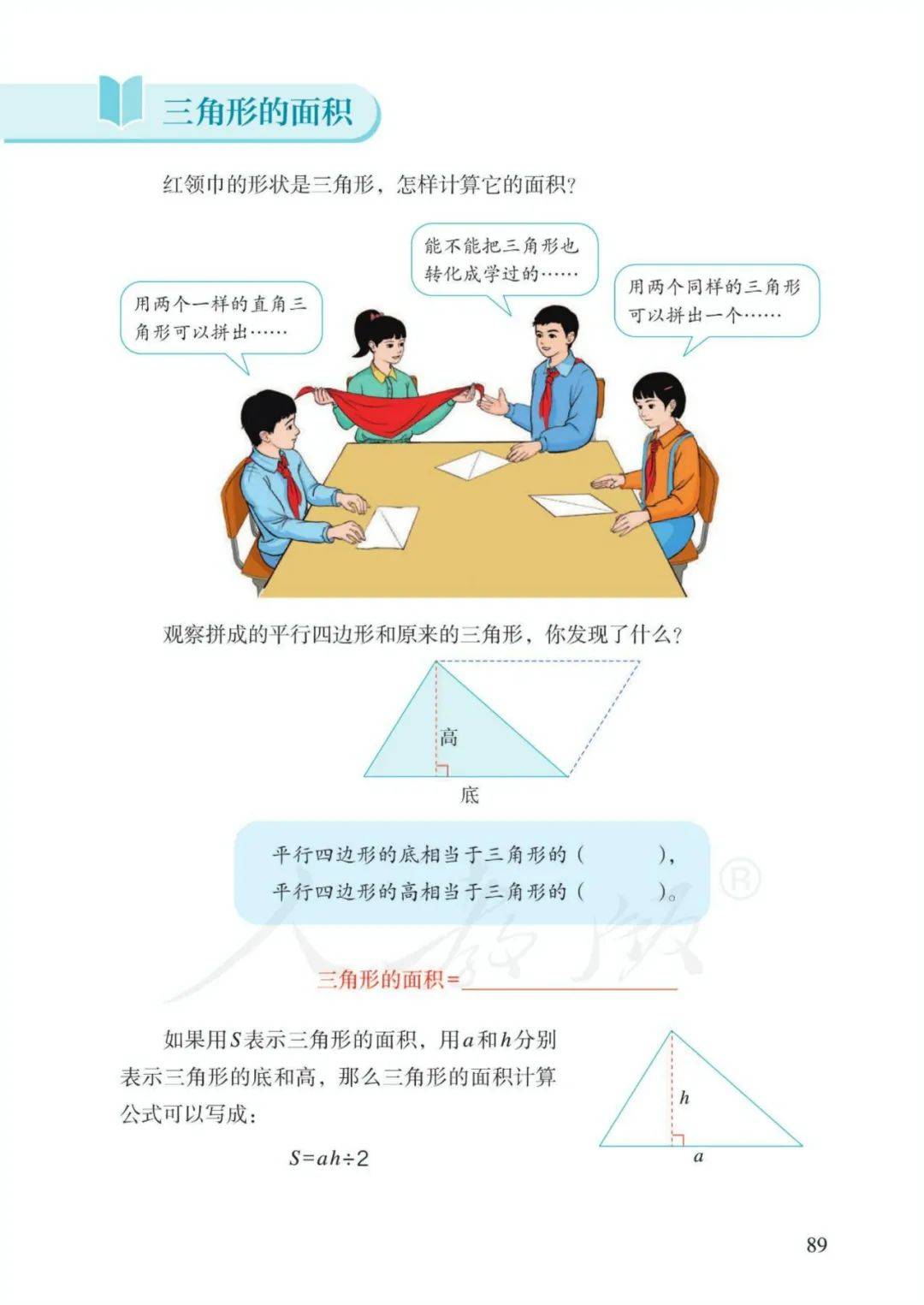
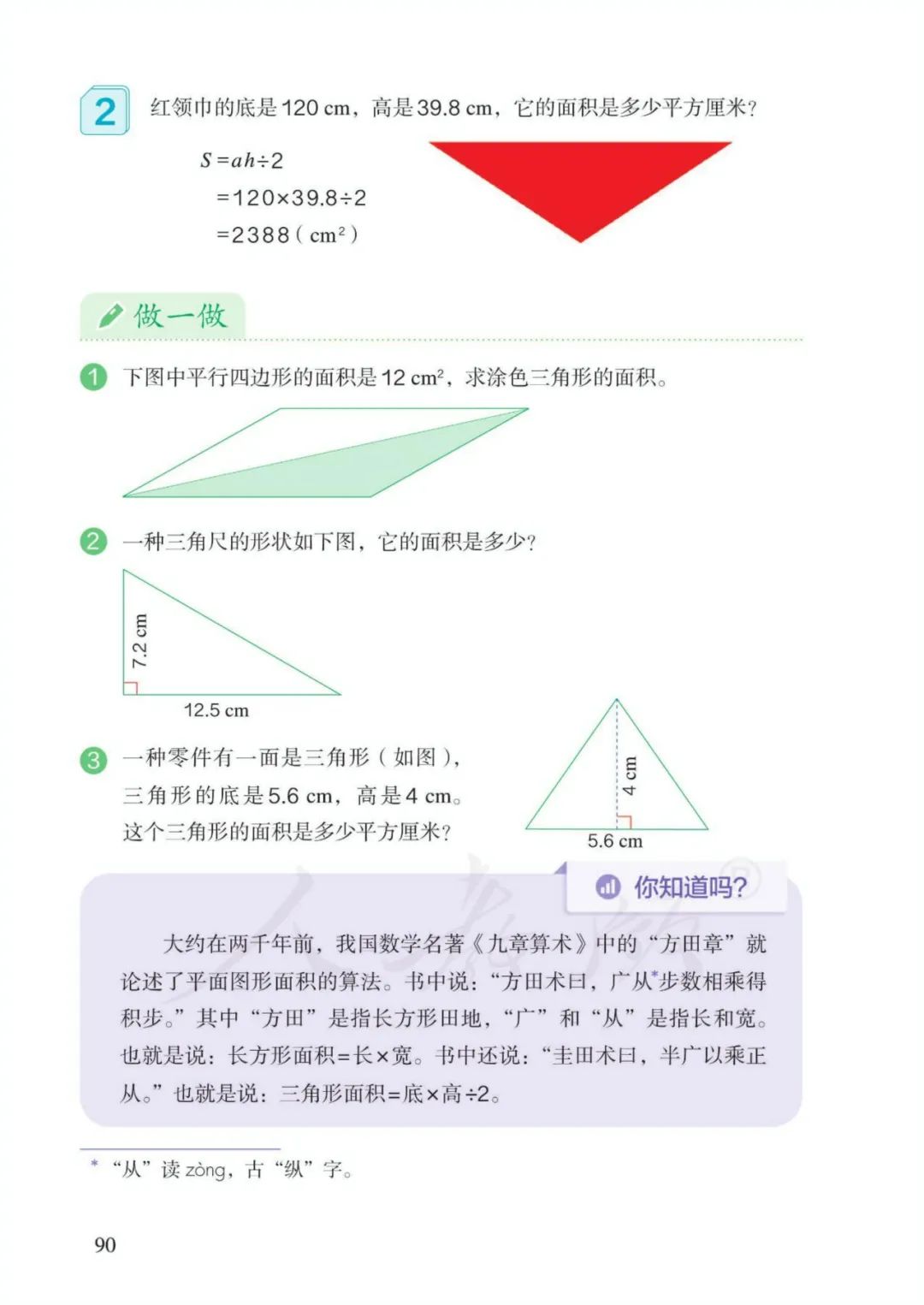
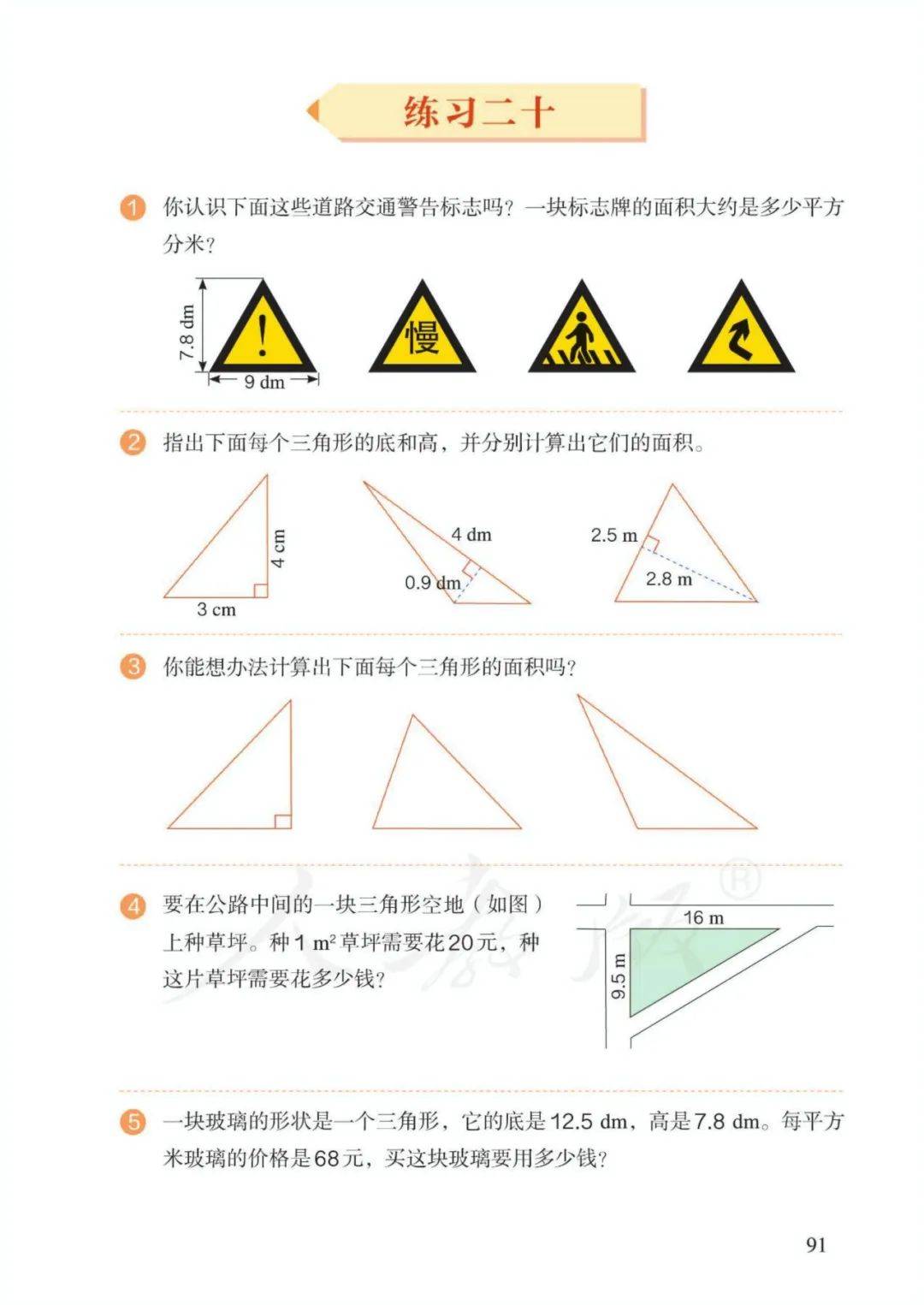
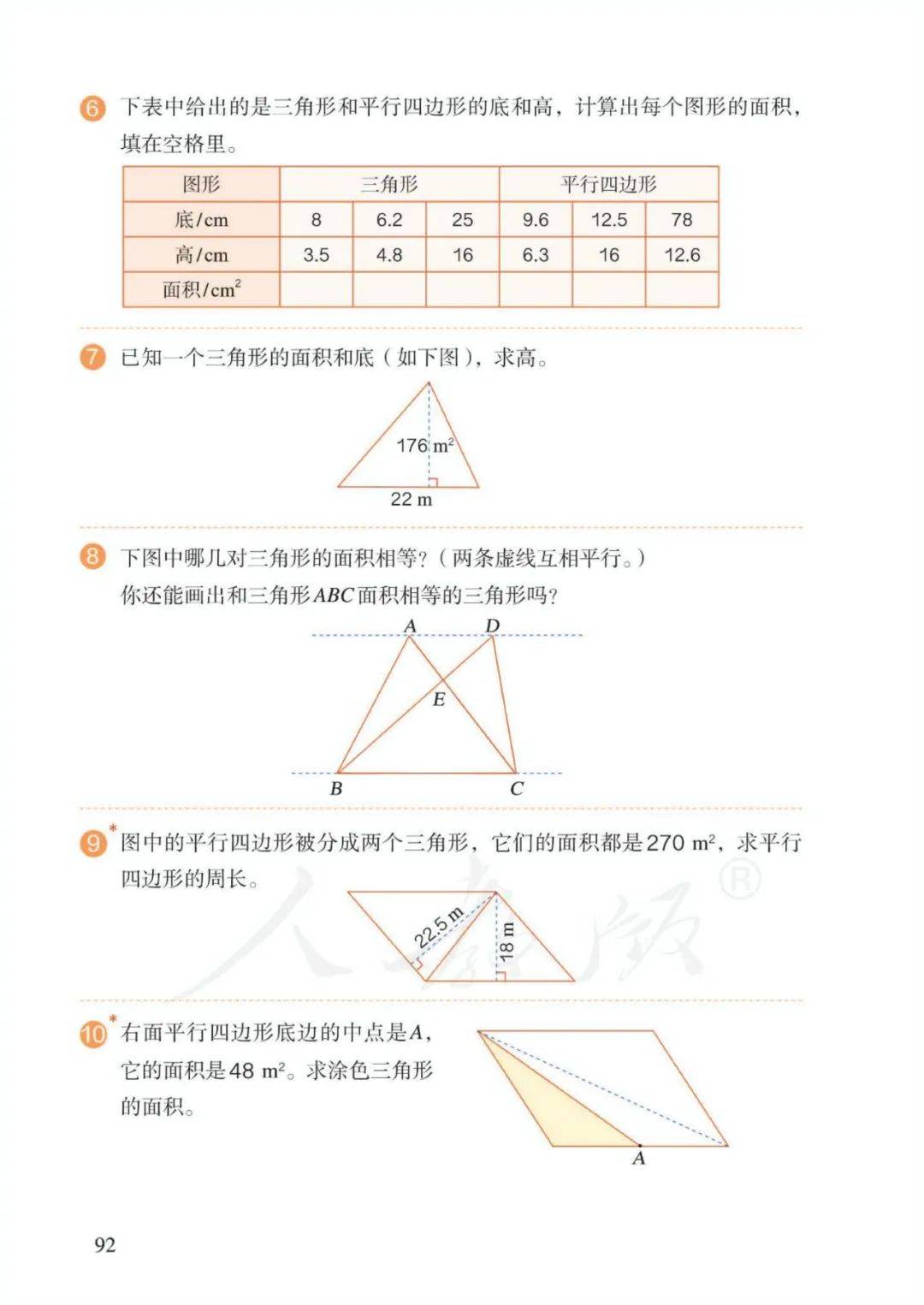
4、三角形的面积=底×高÷2 ——【底=面积×2÷高;高=面积×2÷底】
字母表示: S=ah÷2
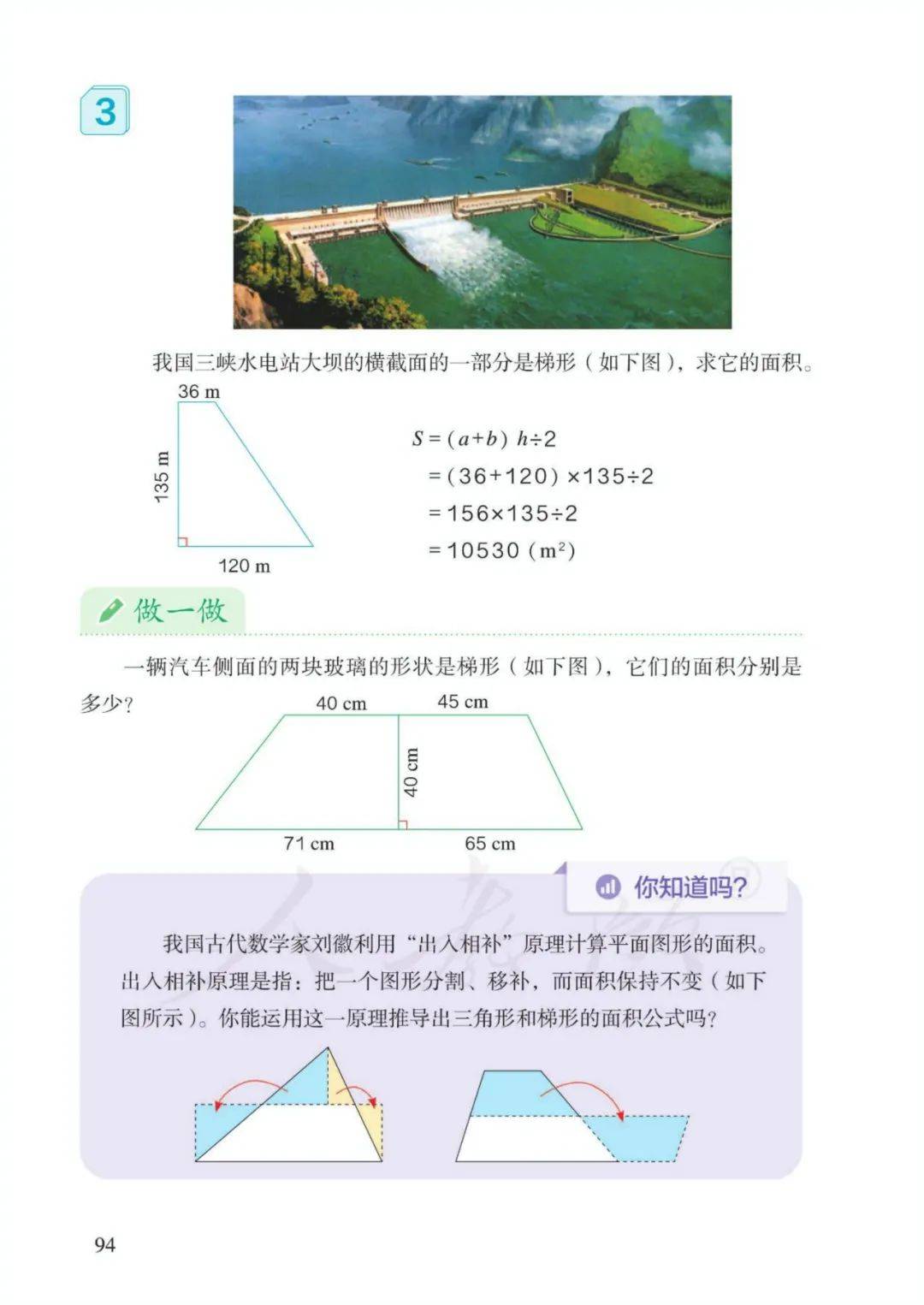
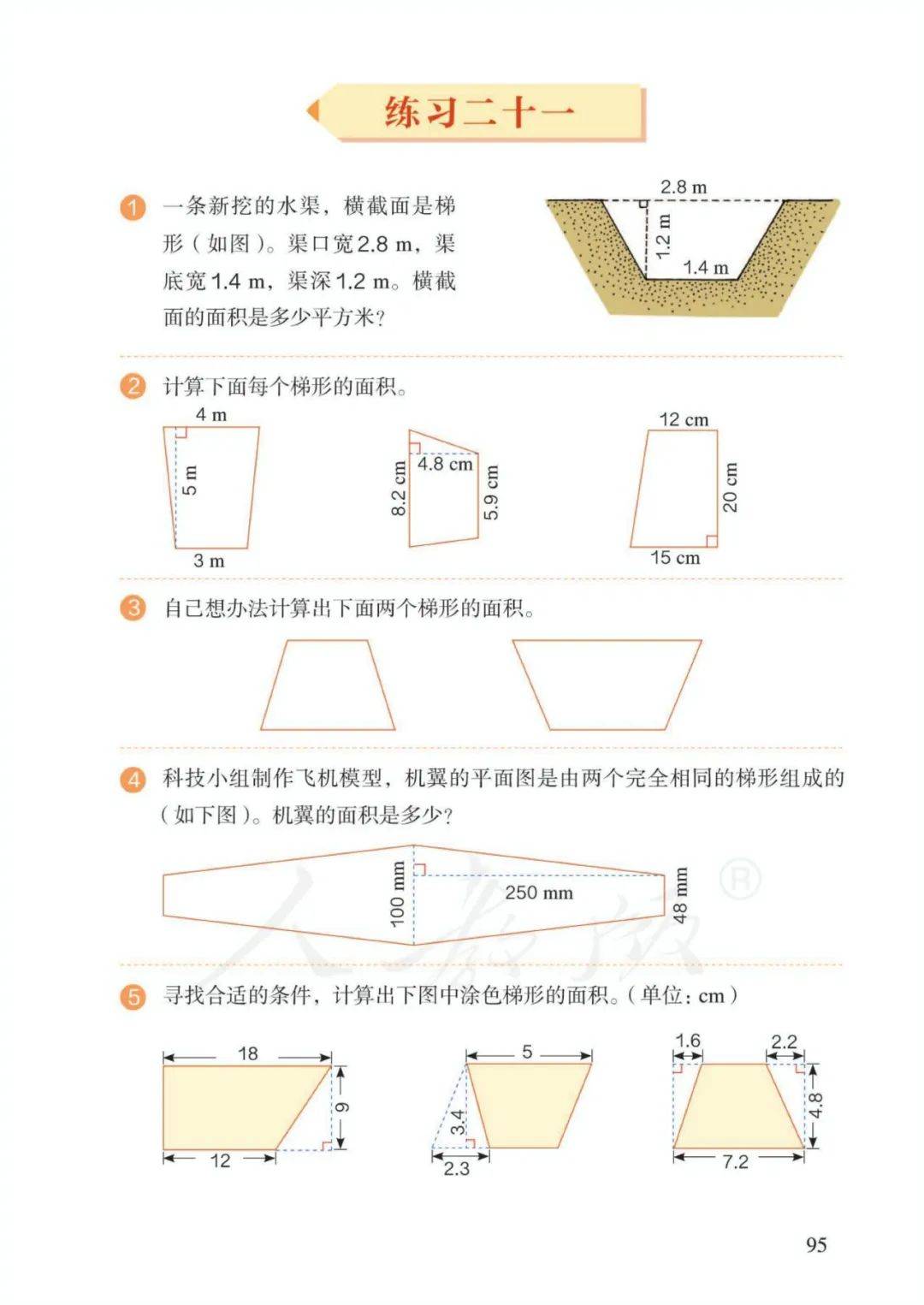
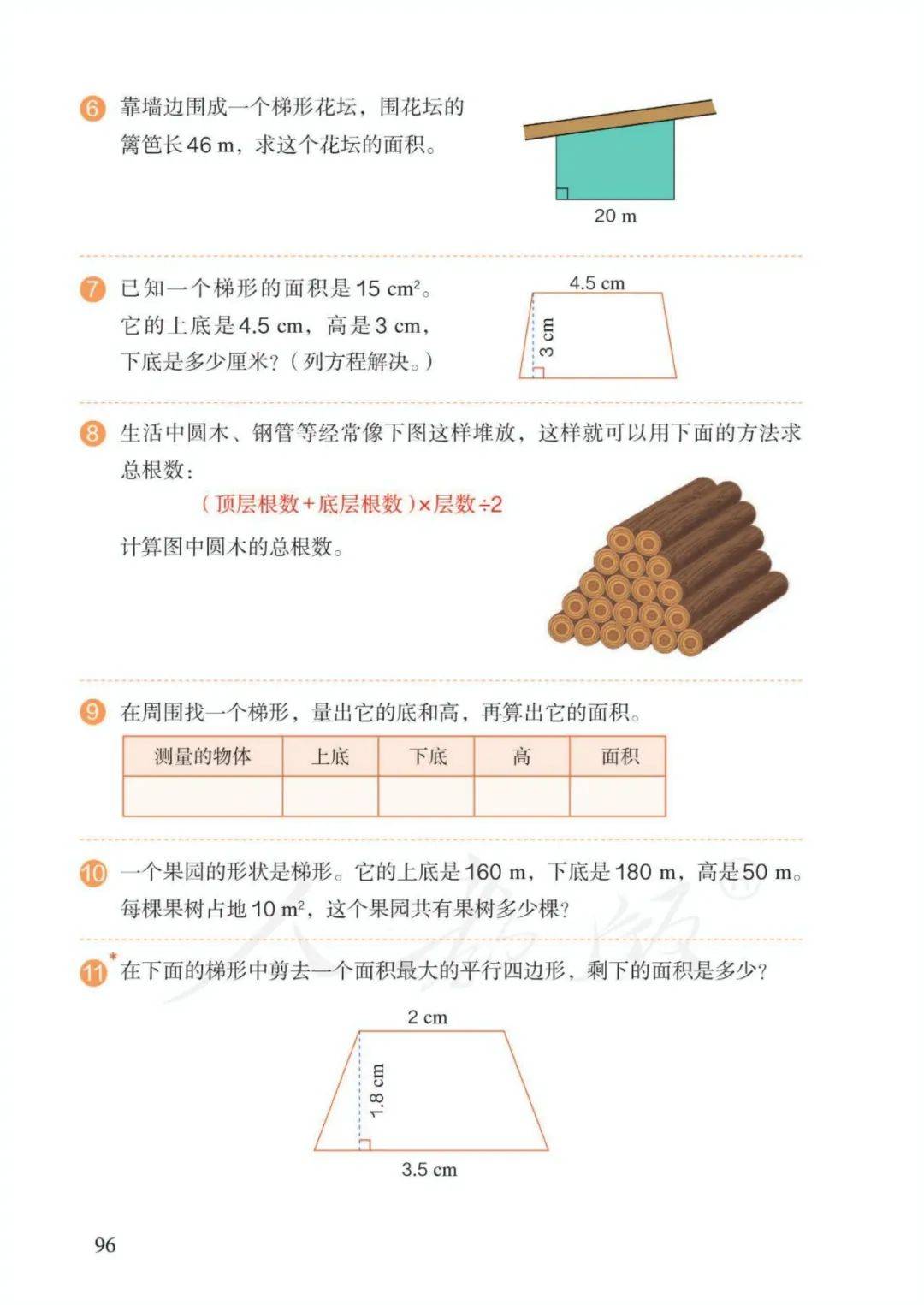
5、梯形的面积=(上底+下底)×高÷2 字母表示: S=(a+b)h÷2
上底=面积×2÷高-下底, 下底=面积×2÷高-上底;
高=面积×2÷(上底+下底)
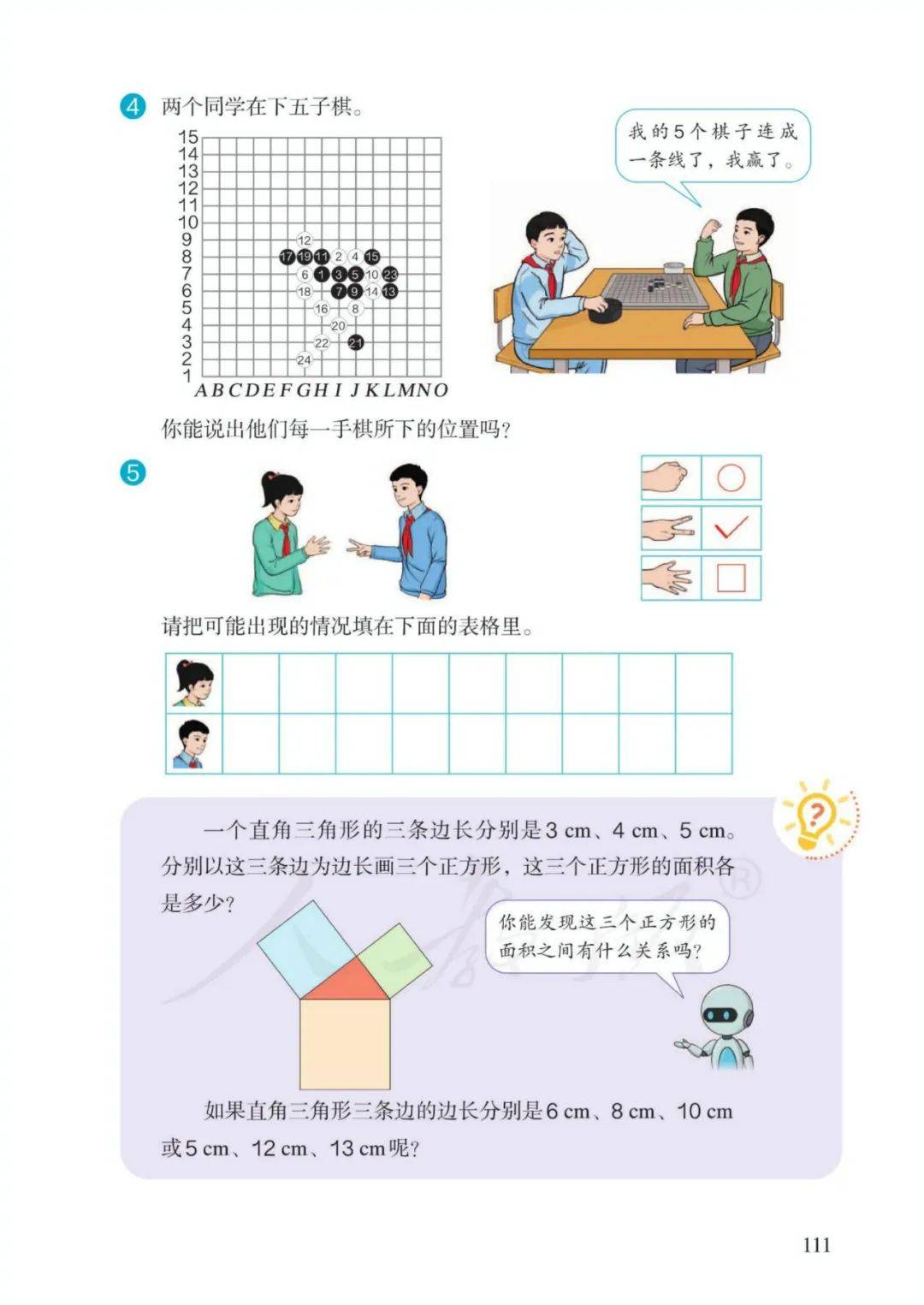
6、平行四边形面积公式推导:剪拼、平移、割补法

7、三角形面积公式推导:旋转、拼凑法
(1)平行四边形可以转化成一个长方形;两个完全一样的三角形可以拼成一个平行四边形,长方形的长相当于平行四边形的底;平行四边形的底相当于三角形的底;长方形的宽相当于平行四边形的高;
(2)平行四边形的高相当于三角形的高;长方形的面积等于平行四边形的面积,平行四边形的面积等于三角形面积的2倍,因为长方形面积=长×宽,所以平行四边形面积=底×高。因为平行四边形面积=底×高,所以三角形面积=底×高÷2
8、梯形面积公式推导:旋转、拼凑法
(1)两个完全一样的梯形可以拼成一个平行四边形;
(2)平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底+下底)×高÷2
9、等底等高的平行四边形面积相等;等底等高的三角形面积相等;
等底等高的平行四边形面积是三角形面积的2倍。
10、长方形框架拉成平行四边形,周长不变,面积变小。
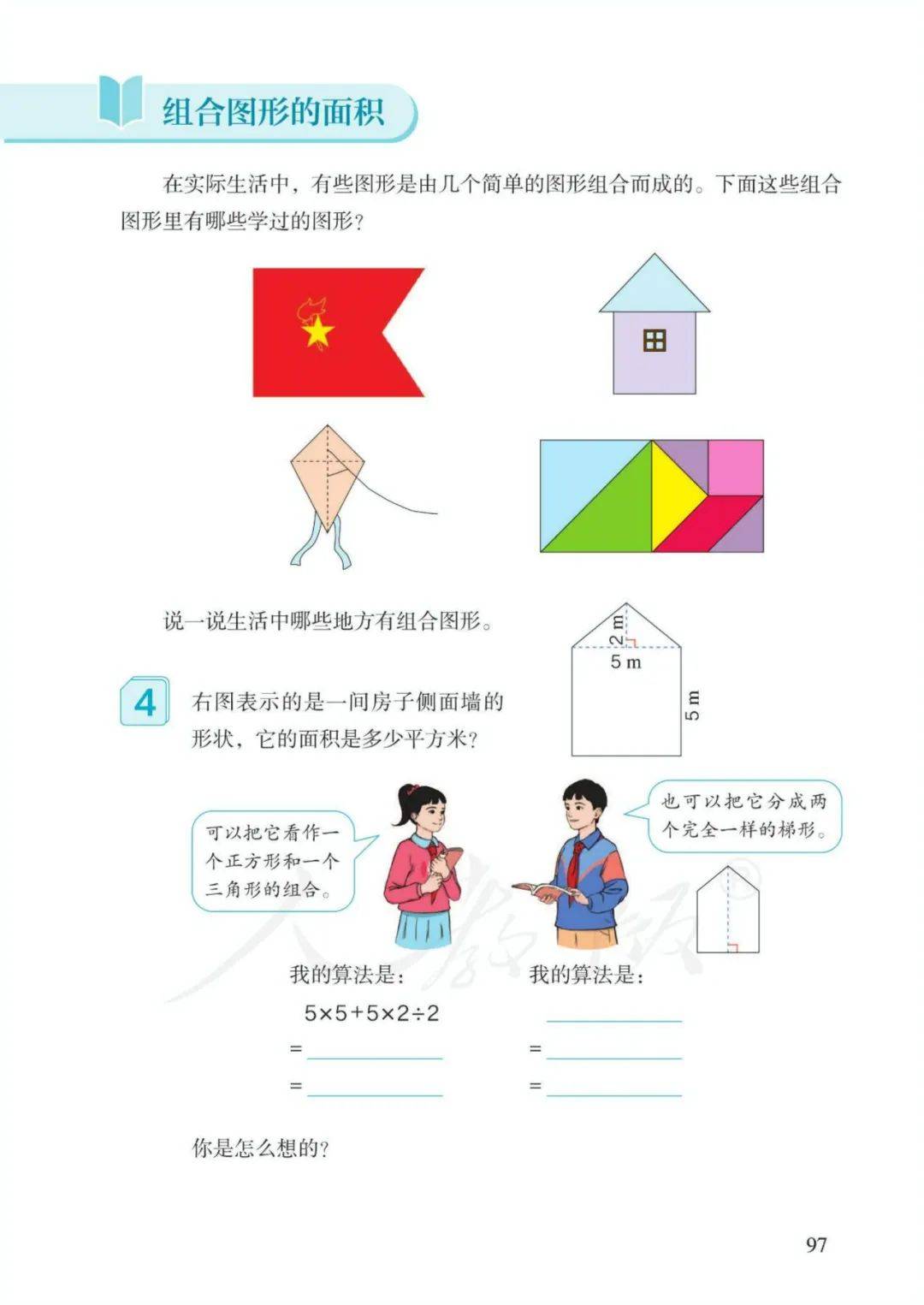
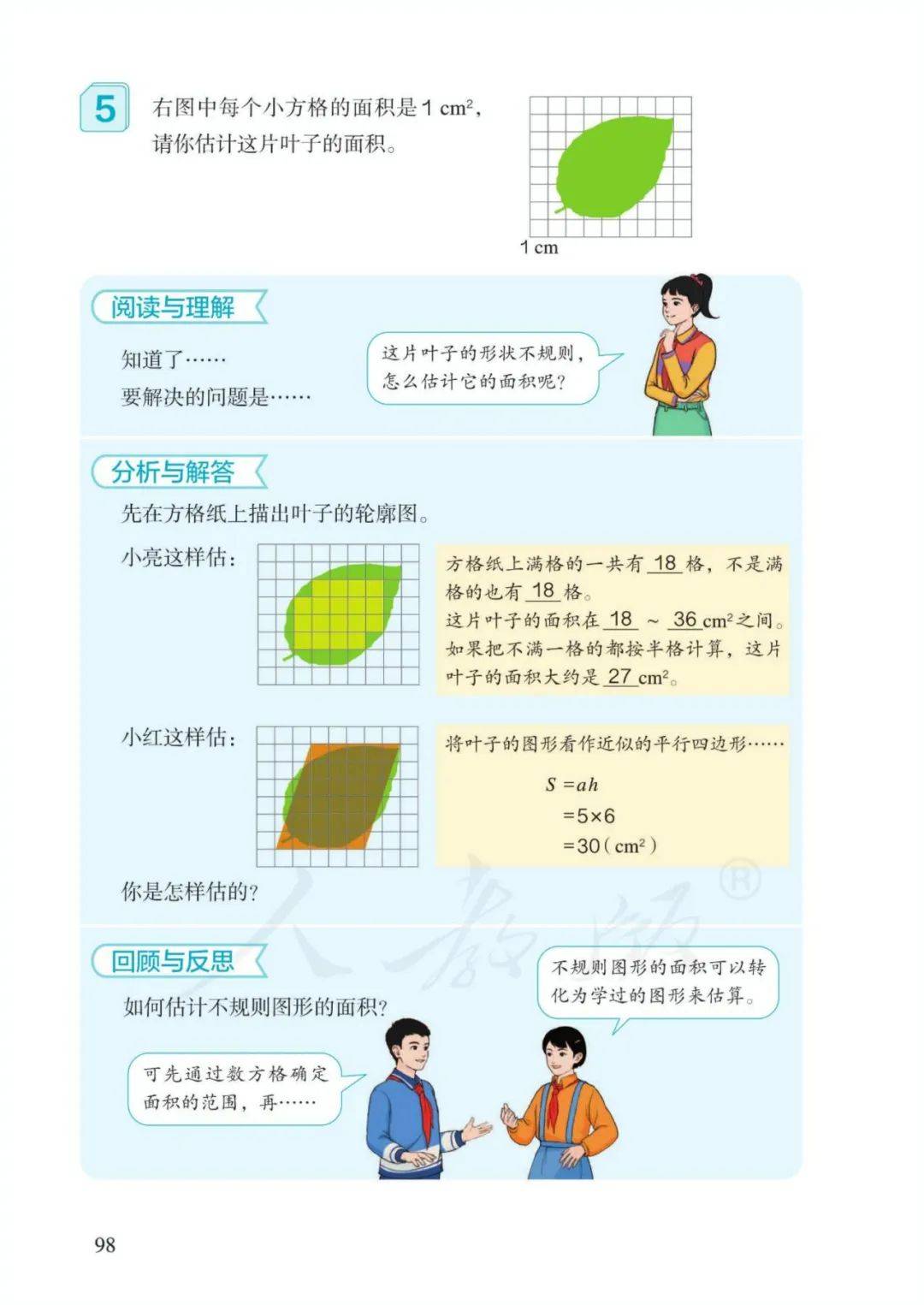
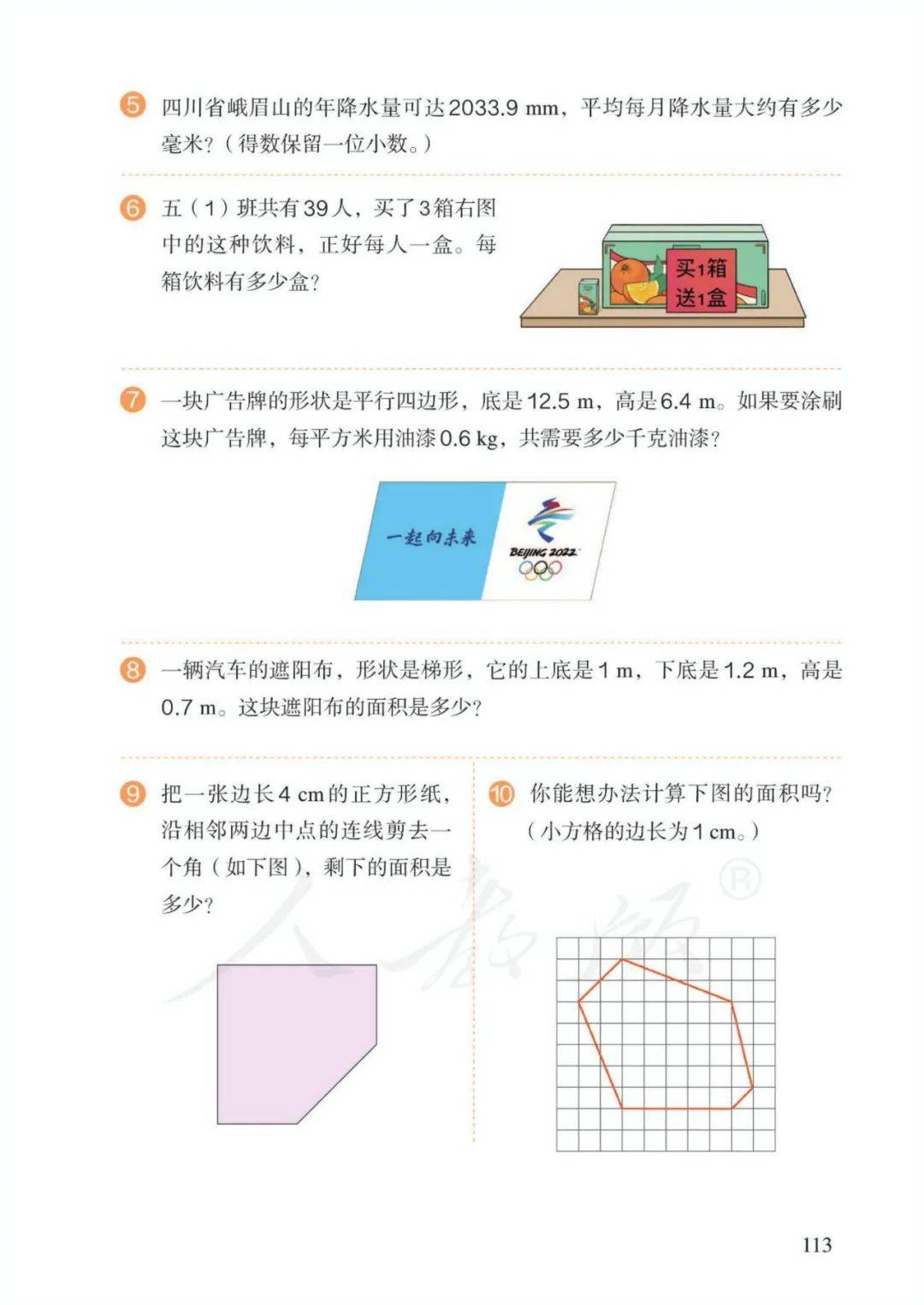
11、组合图形面积(或阴影部分面积):转化成已学的简单图形,通过加、减进行计算(整体-部分=另一部分)。
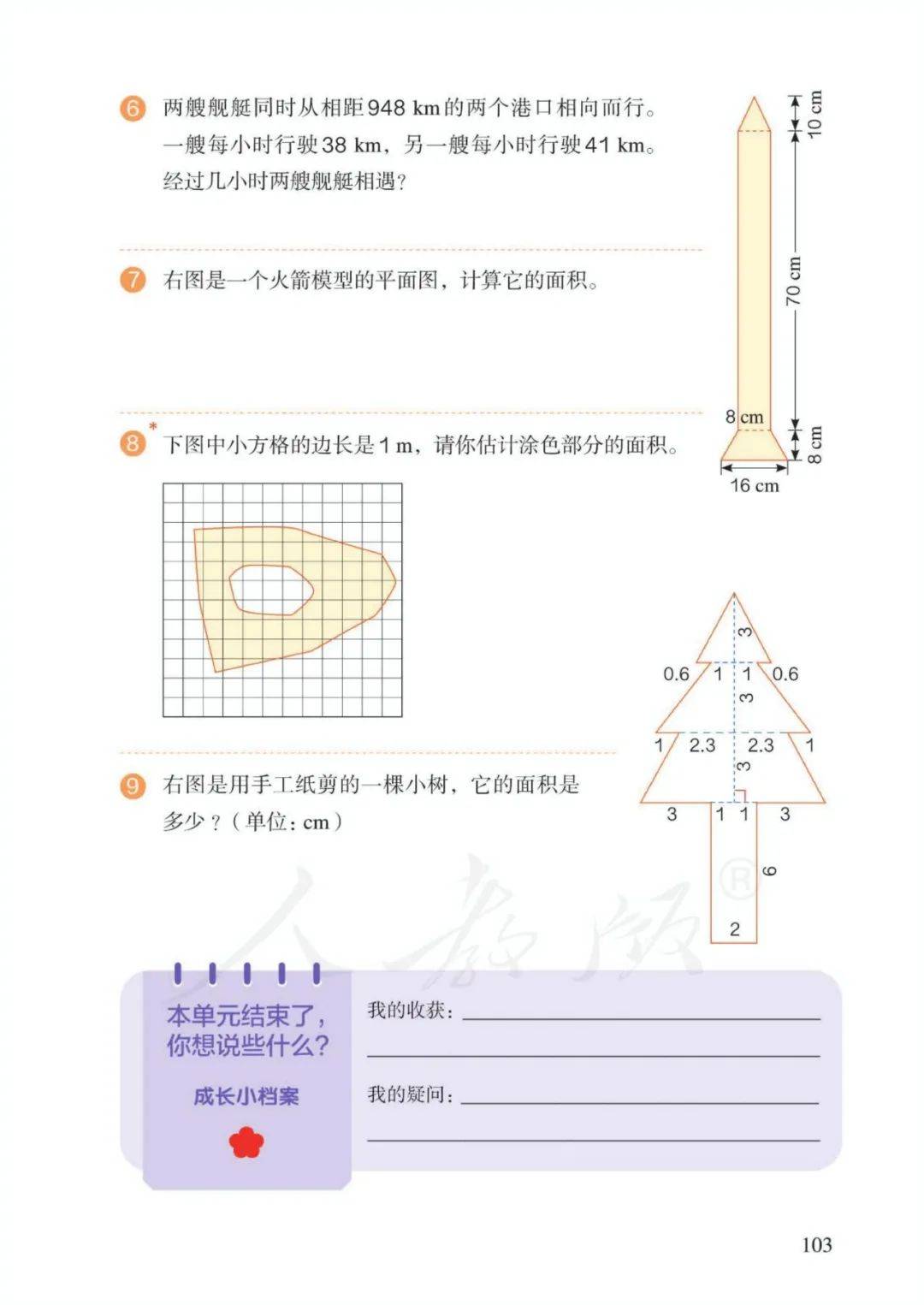
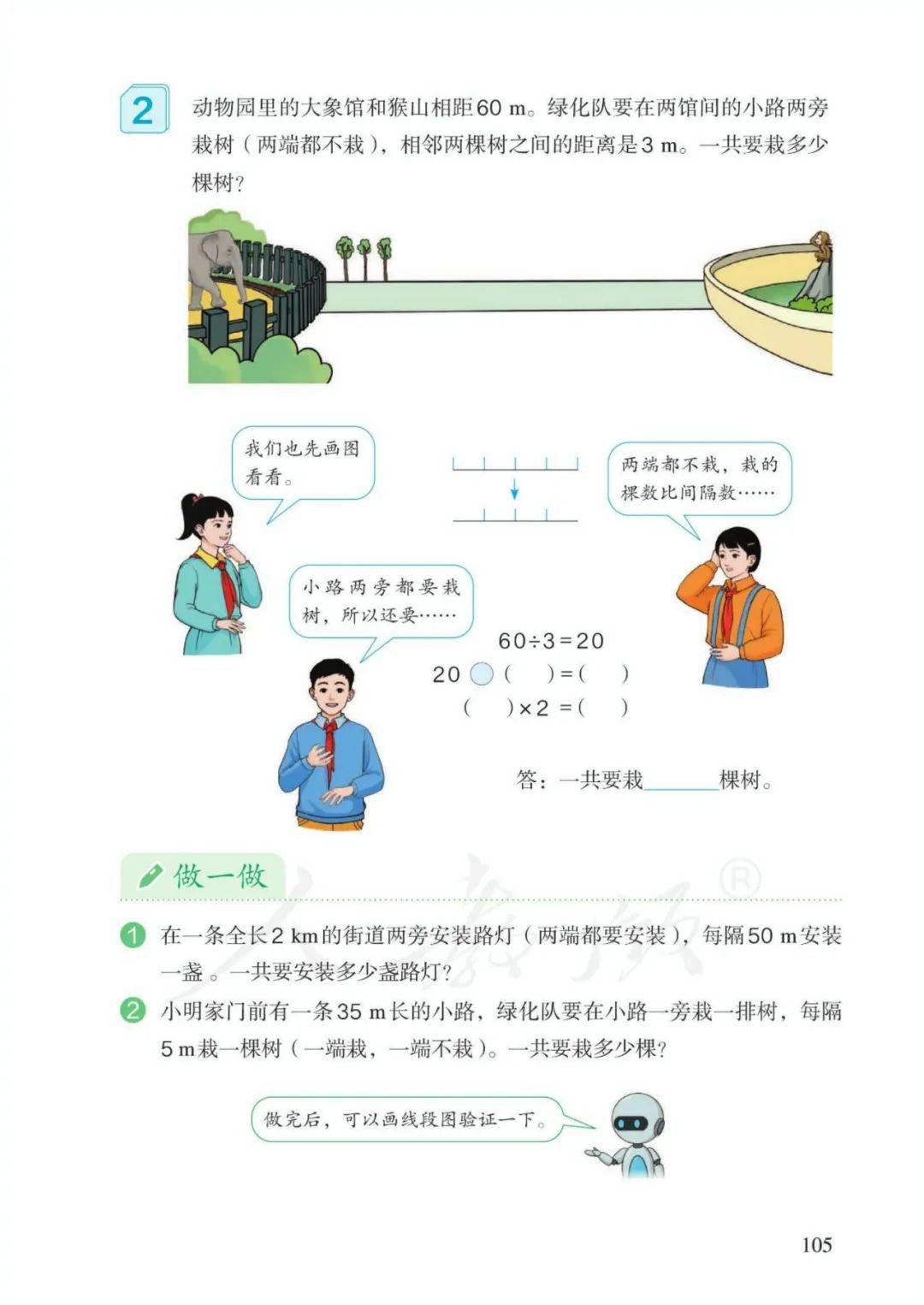
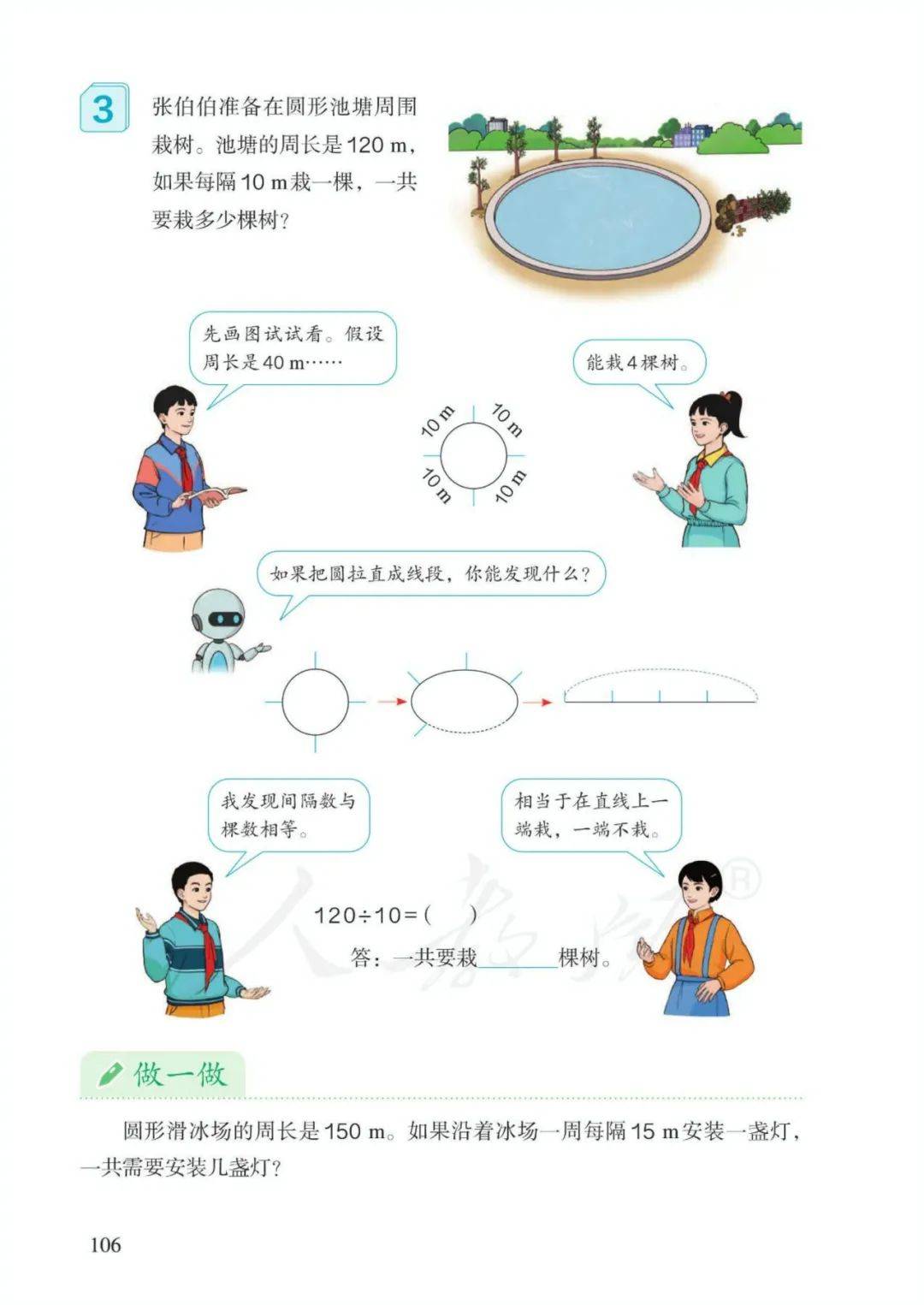
第七单元数学广角——植树问题
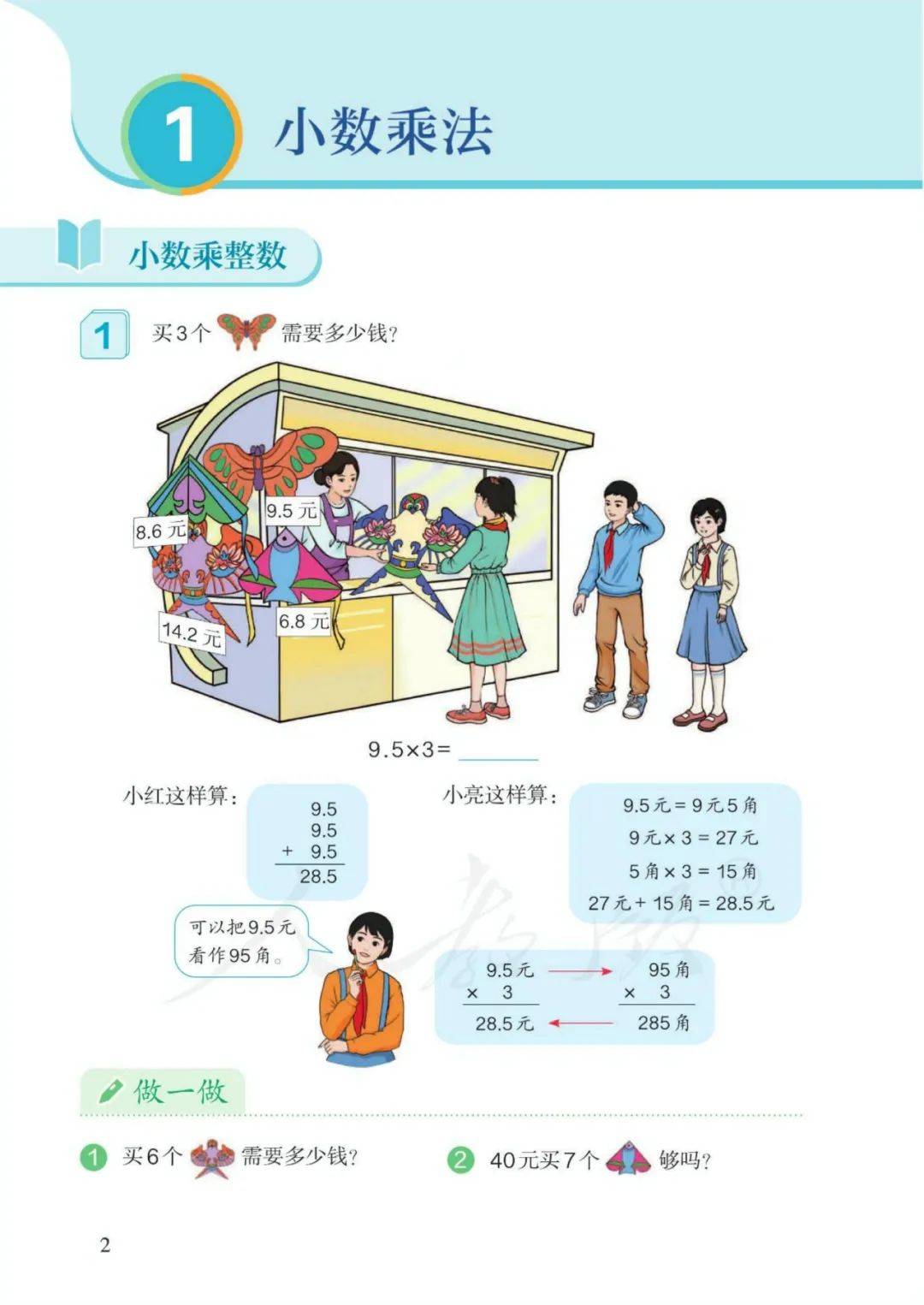
第一单元《小数乘法》知识点
一、小数乘整数 (利用因数的变化引起积的变化规律来计算小数乘法)
知识点一:
1、计算小数加法先把小数点对齐,再把相同数位上的数相加
2、计算小数乘法末尾对齐,按整数乘法法则进行计算。
知识点二:
积中小数末尾有0的乘法。 先计算出小数乘整数的乘积后,积的小数末尾出现0 ,要再根据小数的性质去掉小数末尾的0。如:3.60 “0” 应划去
知识点三:
如果乘得的积的小数位数不够要在前面用0补足,再点上小数点。如0.02×2=0.04
知识点四:
计算整数因数末尾有0的小数乘法时,要把整数数位中不是0的最右侧数字与小数的末尾对齐。
思考:
小数乘整数与整数乘整数有什么不同?
1、小数乘整数中有一个因数是小数,所以积一般来说也是小数。
2 小数乘法中积的小暑部分末尾如有0可以根据小数的基本性质去掉小数末尾的0而整数乘法中是不能去掉的。
二、小数乘小数
知识点一:
因数与积的小数位数的关系:因数中共有几位小数,积中就有几位小数。
知识点二:
小数乘法的一般计算方法:
先按整数乘法算出积,再给积点上小数点(看因数中一共有几位小数,就从积的右边起输出几位,点上小数点。)乘得的积的小数位数不够要在积的前面用0补足,在点小数点。
知识点三:
小数乘法的验算方法
1、把因数的位置交换相乘
2、用计算器来验算
三、积的近似数
知识点一:
先算出积,然后看要保留数位的下一位,再按四舍五入法求出结果,用约等号表示。
知识点二:
如果求得的近似数所求数位的数字是9而后一位数字又大于5需要进1,这是就要依次进一用0占位。如6.597 保留两位为6.60
四、连乘、乘加、乘减
知识点一:
小数乘法要按照从左到右的顺序计算
知识点二:
小数的乘加运算与整数的乘加运算顺序相同。先乘法,后加法
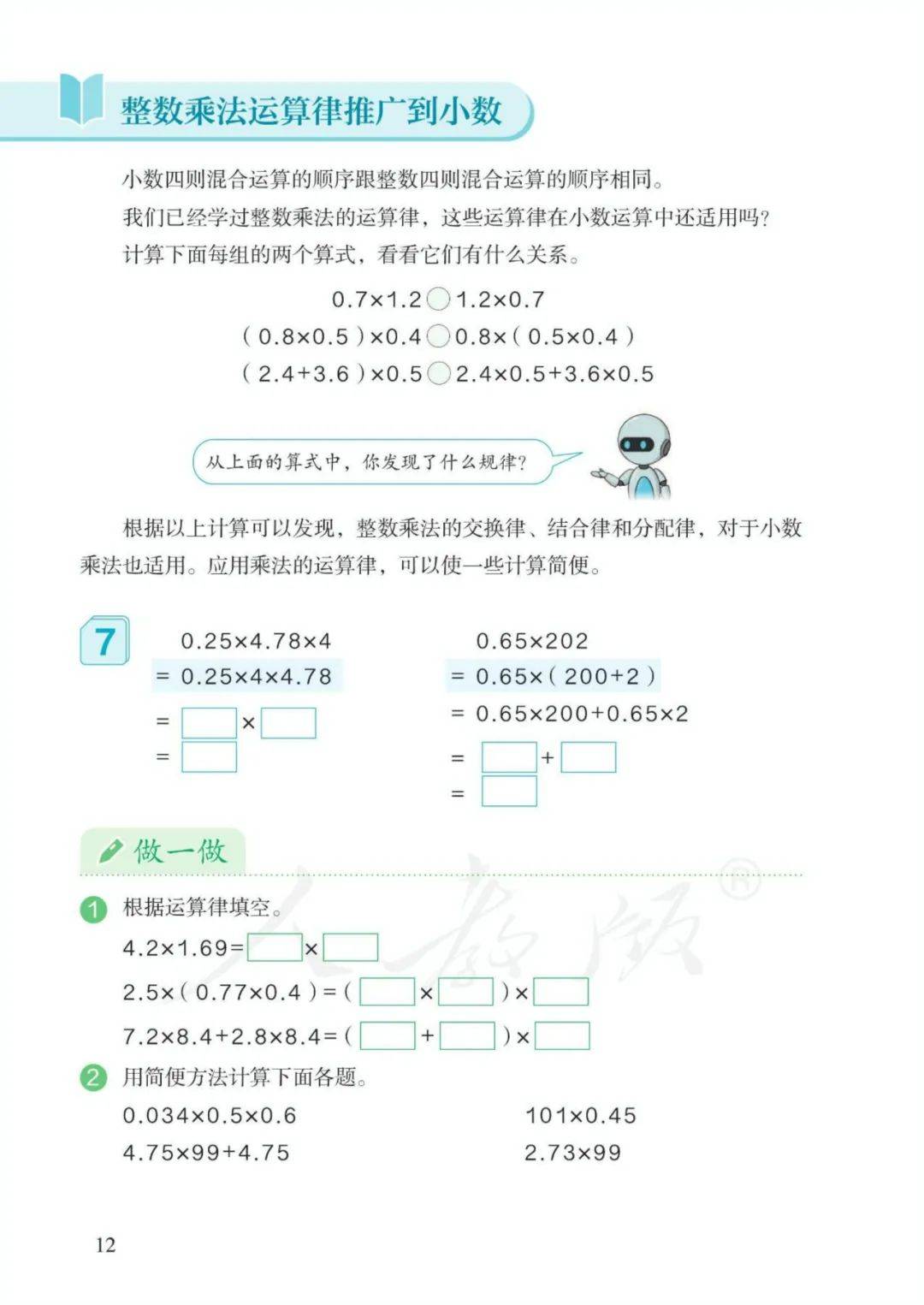
整数乘法的交换律、结合律和分配律,对于小数乘法也适用。
五、简便运算
整数乘法的交换律、结合律和分配律,对于小数乘法也适用
计算连乘法时可应用乘法交换律、结合律将几位整数的两个数先乘,再乘另一个数,计算一步乘法时,可将接近整十、整百的数拆成整十整百的数和一位数相加减的算式,再应用乘法分配律简算。
对于不符合运算定律的算式,有些通过变形也可以应用。
乘法分配律也可以推广到相应的减法。
第二单元《小数除法》知识点
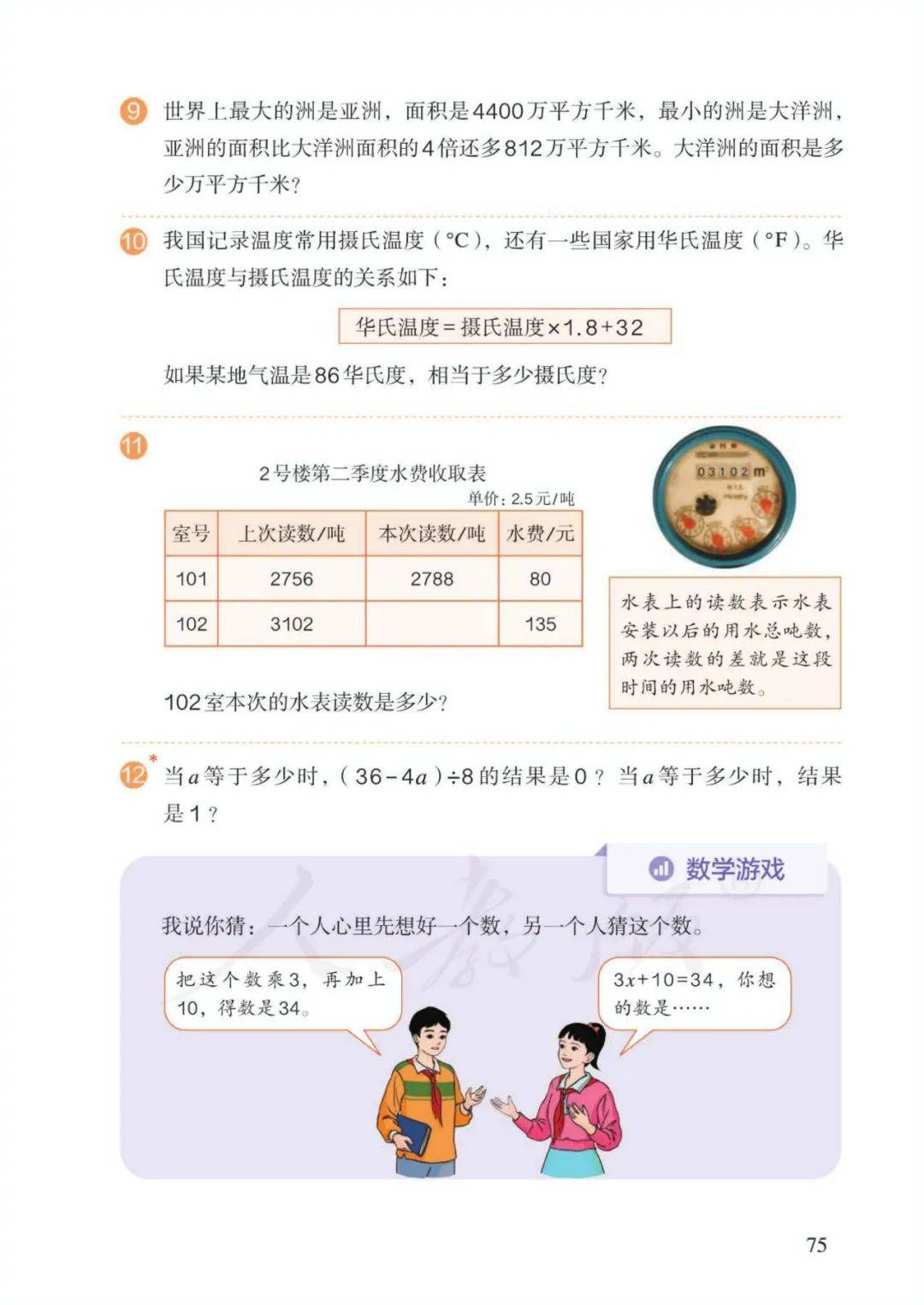
1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。如:2.6÷1.3表示已知两个因数的积2.6与其中的一个因数1.3,求另一个因数的运算。
小数除法的计算方法:
计算除数是整数的小数除法,按整数除法的计算方法去除,商的小数点要和被除数的小数点对齐,整数部分不够除,商0,点上小数点,继续除;如果有余数,要添0再除。
计算除数是小数的除法,先把除数转化成整数,除数的小数点向右移动几位,被除数的小数点也要向右移动几位,位数不够时,在被除数的末尾用0补足,然后按照除数是整数的小数除法进行计算。
2、取近似数的方法:
取近似数的方法有三种,①四舍五入法 ②进一法 ③去尾法
一般情况下,按要求取近似数时用四舍五入法,进一法、去尾法在解决实际问题的时候选择应用。
取商的近似数时,保留到哪一位,一定要除到那一位的下一位,然后用四舍五入的方法取近似数。没有要求时,除不尽的一般保留两位小数。
3、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。依次不断重复出现的数字,叫做这个循环小数的的循环节。
4、循环小数的表示方法:
一种是用省略号表示,要写出两个完整的循环节,后面标上省略号。如:0.3636…… 1.587587……
另一种是简写的方法:即只写出一组循环节,然后在循环节的第一个数字和最后一个数上面点上圆点。如:12.
5、有限小数:小数部分的位数是有限的小数,叫做有限小数。
6、无限小数:小数部分的位数是无限的小数,叫做无限小数。
第三单元《观察物体》知识点
1、从不同的角度观察物体,看到的形状可能是不同的;观察长方体或正方体时,从固定位置最多能看到三个面。
2、正面、侧面、后面都是相对的,它是随着观察角度的变化而变化。通过观察、想象、猜测,培养空间想象力和思维能力,能正确辨认从正面、侧面、上面观察到的简单物体的形状。
3、构建空间想象力:
(1)、将两个完全一样的正方体并排放,要求想象画出以不同角度看到的样子(强调左右面是重合,故只能看见一个正方形)。
(2)、将一个正方体和圆柱体并排放,要求想象画出从不同角度看到的样子。
4、动手操作,思维拓展
用5个小正方体摆从正面看到的图形(你能摆出几种不同的方法)。(有多少种不同摆法,最少要用多少个小正方体,最多只能用多少个小正方体。)
第四单元《简易方程》知识点
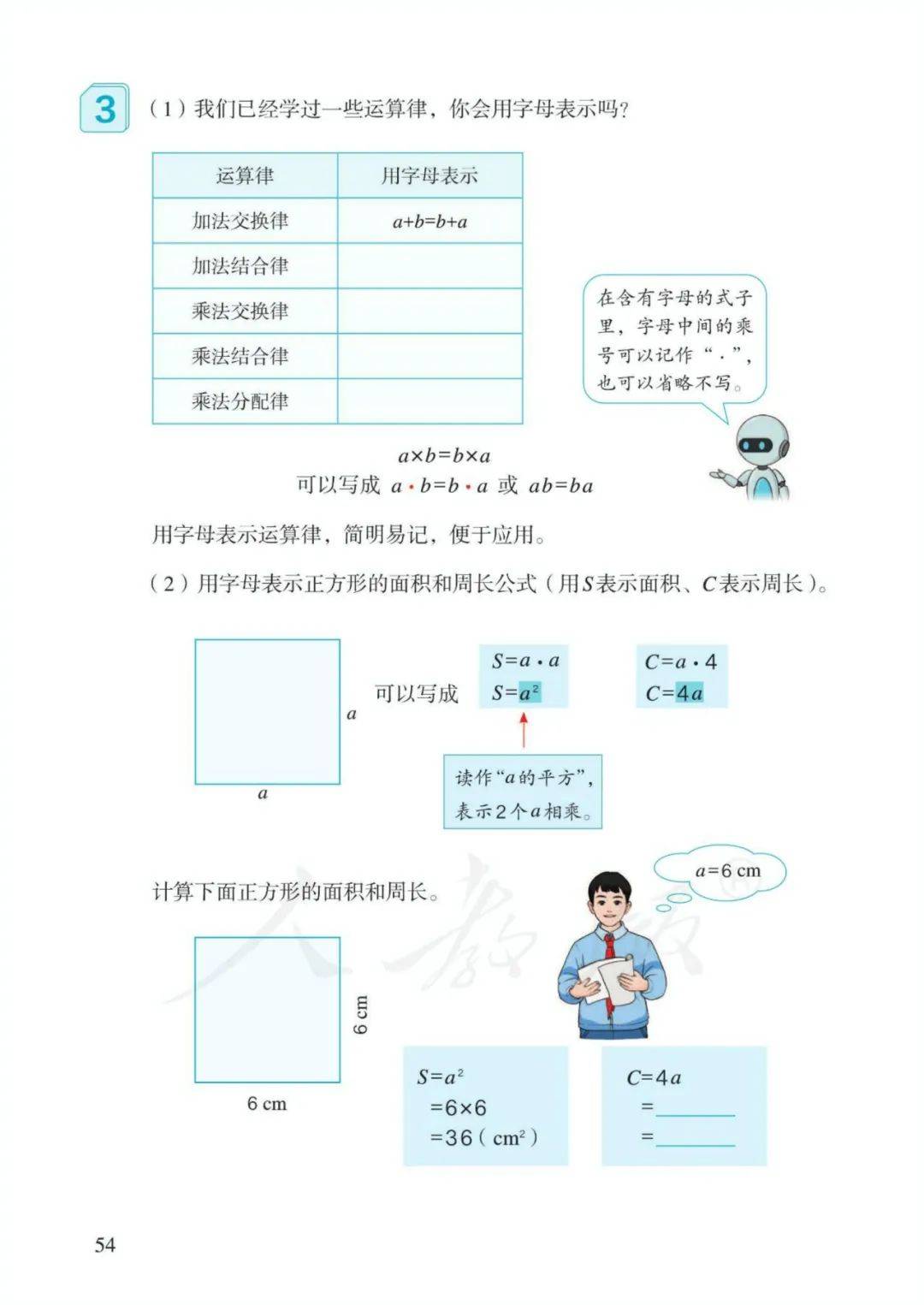
1、用字母表运算定律。
加法交换律: a+b=b+a 加法结合律: a+b+c=a+(b+c)
乘法交换律: a×b=b×a 乘法结合律:a×b×c=a×(b×c)
乘法分配律: (a±b)×c=a×c±b×c
2、用字母表示计算公式。
长方形的周长公式: c=(a+b)×2 长方形的面积公式: s=ab
正方形的周长公式: c=4a 正方形的面积公式: s=
3、 读作:x的平方,表示:两个x相乘。
2x表示:两个x相加,或者是2乘x。
4、①含有未知数的等式称为方程。
②使方程左右两边相等的未知数的值叫做方程的解。
③求方程的解的过程叫做解方程。
5、把下面的数量关系补充完整。
路程=(速度)×(时间) 速度=(路程)÷(时间) 时间=(路程)÷(速度)
总价=(单价)×(数量) 单价=(总价)÷(数量) 数量=(总价)÷(单价)
总产量=(单产量)×(数量) 单产量=(总产量)÷(数量)
数量=(总产量)÷(单价 )
工作总量=(工作效率)×(工作时间)
工作效率=(工作总量)÷(工作时间)
工作时间=(工作总量)÷(工作效率)
大数-小数=相差数 大数-相差数=小数 小数+相差数=大数
一倍量×倍数=几倍量 几倍量÷倍数=一倍量
几倍量÷一倍量=倍数
被减数=减数+差 减数=被减数-差 加数=和-另一个加数
被除数=除数×商 除数=被除数÷商 因数=积÷另一个因数
第五单元 《多边形面积》知识点
1、长方形面积=长×宽 字母公式:s=ab
长方形周长=(长+宽)×2 字母公式:c=(a+b)×2
2、正方形面积=边长×边长 字母公式:s= 或者s=a×a
正方形周长=边长×4 字母公式:c=4a 或者c= a×4
3、平行四边形面积=底×高 字母公式:s=ah
4、三角形面积=底× 高÷2 字母公式:s=ah÷2
5、梯形面积=(上底+下底)×高÷2 字母公式:s=(a+b)×h÷2
6、计算圆木、钢管等的根数: (顶层根数+底层根数)×层数÷2
7、等底等高的平行四边形面积相等。等底等高的三角形面积相等。
等底等高的三角形和平行四边形面积关系:三角形的面积是平行四边形面积的一半,平行四边形的面积是三角形面积的2倍。
8、组合图形:转化成已学的简单图形,通过加、减进行计算。
第六单元《统计与可能性》知识点
1、平均数=总数量÷总份数
2、中位数的优点是不受偏大或偏小数据的影响,用它代表全体数据的一般水平更合适
第七单元《数学广角》知识点
1、数不仅可以用来表示数量和顺序,还可以用来编码。
2、邮政编码:由6位组成,前2位表示省(直辖市、自治区),前3位表示邮区,前4位表示县(市),最后2位表示投递局(所)。
3、身份证号码:由18位组成,(1)前1、2位数字表示:所在省份的代码; (2)第3、4位数字表示:所在城市的代码;
(3)第5、6位数字表示:所在区县的代码;
(4)第7~14位数字表示:出生年、月、日;
(5)第15、16位数字表示:所在地的派出所的代码;
(6)第17位数字表示性别:奇数表示男性,偶数表示女性;
(7)第18位数字是校检码: 用来检验身份证的正确性。校检码可以是0~9的数字,有时也用x表示。










